Series geométricas - Geometric series

La serie geométrica 1/4 + 1/16 + 1/64 + 1/256 + ... se muestra como áreas de cuadrados morados. Cada uno de los cuadrados morados tiene 1/4 del área del siguiente cuadrado más grande ( 1/2 × 1/2 = 1/4, 1/4 × 1/4 = 1/16, etc.). La suma de las áreas de los cuadrados morados es un tercio del área del cuadrado grande.

Otra serie geométrica (coeficiente a = 4/9 y razón común r = 1/9) se muestra como áreas de cuadrados morados. El área púrpura total es S = a / (1 - r ) = (4/9) / (1 - (1/9)) = 1/2, lo que puede confirmarse observando que el cuadrado exterior está dividido en un infinito. número de áreas en forma de L, cada una con cuatro cuadrados morados y cuatro cuadrados amarillos, que es mitad morado.

En matemáticas , una serie geométrica es la suma de un número infinito de términos que tienen una razón constante entre términos sucesivos. Por ejemplo, la serie

${\ Displaystyle {\ frac {1} {2}} \, + \, {\ frac {1} {4}} \, + \, {\ frac {1} {8}} \, + \, {\ frac {1} {16}} \, + \, \ cdots}$

es geométrico, porque cada término sucesivo se puede obtener multiplicando el término anterior por 1/2. En general, una serie geométrica se escribe como a + ar + ar ² + ar ³ + ..., donde a es el coeficiente de cada término yr es la razón común entre términos adyacentes. Las series geométricas se encuentran entre los ejemplos más simples de series infinitas y pueden servir como una introducción básica a las series de Taylor y Fourier . Las series geométricas tuvieron un papel importante en el desarrollo temprano del cálculo , se utilizan en todas las matemáticas y tienen aplicaciones importantes en física , ingeniería , biología , economía , informática , teoría de colas y finanzas .

La distinción entre una progresión y una serie es que una progresión es una secuencia, mientras que una serie es una suma.

Coeficiente a

Los primeros nueve términos de la serie geométrica 1 + r + r ² + r ³ ... dibujados como funciones (coloreadas en el orden rojo, verde, azul, rojo, verde, azul, ...) dentro del rango -1 < r <1. La serie geométrica de forma cerrada 1 / (1 - r ) es la línea discontinua negra.

La serie geométrica a + ar + ar ² + ar ³ + ... se escribe en forma expandida. Todos los coeficientes de la serie geométrica son iguales. En contraste, las series de potencia escriben como un ₀ + un ₁ r + un ₂ r ² + un ₃ r ³ + ... en forma expandida tiene coeficientes de un _i que puede variar de término a término. En otras palabras, la serie geométrica es un caso especial de la serie de potencias. El primer término de una serie geométrica en forma expandida es el coeficiente a de esa serie geométrica.

Además de la forma expandida de la serie geométrica, existe una forma generadora de la serie geométrica escrita como

${\ Displaystyle \ sum _ {k = 0} ^ {\ infty}}$ ar ^k

y una forma cerrada de la serie geométrica escrita como

a / (1 - r ) dentro del rango | r | <1.

La derivación de la forma cerrada a partir de la forma expandida se muestra en la sección Suma de este artículo . La derivación requiere que todos los coeficientes de la serie sean iguales (coeficiente a) para aprovechar la auto-similitud y reducir el número infinito de adiciones y operaciones de potencia en la forma expandida a la resta simple y división simple en la forma expandida. forma cerrada. Sin embargo, incluso sin que la derivación, el resultado puede ser confirmado con la división larga : un dividido por (1 - r ) resulta en un + ar + ar ² + ar ³ + ..., que es la forma expandida de la serie geométrica.

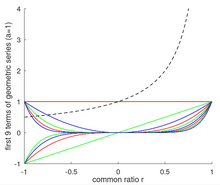
Normalmente, una serie geométrica se considera una suma de números a + ar + ar ² + ar ³ + ... pero también se puede pensar como una suma de funciones a + ar + ar ² + ar ³ + ... que converge a la función a / (1 - r ) dentro del rango | r | <1. La imagen adyacente muestra la contribución de cada uno de los primeros nueve términos (es decir, funciones) a la función a / (1 - r ) dentro del rango | r | <1 cuando a = 1. Cambiar incluso uno de los coeficientes a algo diferente al coeficiente a (además de cambiar la serie geométrica a una serie de potencias) cambiaría la suma de funciones resultante a alguna función distinta de a / (1 - r ) dentro del rango | r | <1. Como acotación al margen, un cambio particularmente útil en los coeficientes lo define la serie de Taylor , que describe cómo cambiar los coeficientes para que la suma de funciones converja a cualquier función seleccionada por el usuario, suficientemente suave dentro de un rango.

Razón común r

La convergencia de la serie geométrica con r = 1/2 y a = 1/2

La convergencia de la serie geométrica con r = 1/2 y a = 1

Vista de cerca de la suma acumulada de funciones dentro del rango -1 < r <-0.5 a medida que se agregan los primeros 11 términos de la serie geométrica 1 + r + r ² + r ³ + ... La serie geométrica 1 / (1 - r ) es la línea discontinua roja.

Reproducir medios

Serie geométrica compleja (coeficiente a = 1 y razón común r = 0.5 e ^{iω ₀ t} ) que convergen en un círculo. En la animación, cada término de la serie geométrica se dibuja como un vector dos veces : una vez en el origen y nuevamente dentro de la suma vectorial de cabeza a cola que converge al círculo. El círculo interseca el eje real en 2 (= 1 / (1-1 / 2) cuando θ = 0) y en 2/3 (= 1 / (1 - (- 1/2)) cuando θ = 180 grados).

La serie geométrica a + ar + ar ² + ar ³ + ... es una serie infinita definida por solo dos parámetros : coeficiente a y razón común r . La razón común r es la razón de cualquier término con el término anterior de la serie. O de manera equivalente, la razón común r es el término multiplicador que se usa para calcular el siguiente término de la serie. La siguiente tabla muestra varias series geométricas:

La convergencia de la serie geométrica depende del valor de la razón común r :

• Si | r | <1, los términos de la serie se acercan a cero en el límite (haciéndose cada vez más pequeños en magnitud ), y la serie converge a la suma a / (1 - r ).
• Si | r | = 1, la serie no converge. Cuando r = 1, todos los términos de la serie son iguales y la serie es infinita. Cuando r = −1, los términos toman dos valores alternativamente (por ejemplo, 2, −2, 2, −2, 2, ...). La suma de los términos oscila entre dos valores (por ejemplo, 2, 0, 2, 0, 2, ...). Este es un tipo diferente de divergencia. Ver, por ejemplo, la serie de Grandi : 1 - 1 + 1 - 1 + ···.
• Si | r | > 1, los términos de la serie se vuelven más y más grandes en magnitud. La suma de los términos también aumenta cada vez más y la serie no converge en una suma. (La serie diverge .)

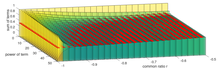
La tasa de convergencia también depende del valor de la razón común r . Específicamente, la tasa de convergencia se vuelve más lenta a medida que r se acerca a 1 o −1. Por ejemplo, la serie geométrica con a = 1 es 1 + r + r ² + r ³ + ... y converge a 1 / (1 - r ) cuando | r | <1. Sin embargo, el número de términos necesarios para converger se acerca al infinito cuando r se acerca a 1 porque a / (1 - r ) se acerca al infinito y cada término de la serie es menor o igual a uno. Por el contrario, a medida que r se acerca a -1, la suma de los primeros términos de la serie geométrica comienza a converger a 1/2, pero cambia ligeramente hacia arriba o hacia abajo dependiendo de si el término agregado más recientemente tiene una potencia de r que es par o impar. . Ese comportamiento de volteo cerca de r = −1 se ilustra en la imagen adyacente que muestra los primeros 11 términos de la serie geométrica con a = 1 y | r | <1.

La razón común r y el coeficiente a también definen la progresión geométrica , que es una lista de los términos de la serie geométrica pero sin las adiciones. Por lo tanto, la serie geométrica a + ar + ar ² + ar ³ + ... tiene la progresión geométrica (también llamada secuencia geométrica) a , ar , ar ² , ar ³ , ... La progresión geométrica - tan simple como es - modela un sorprendente número de fenómenos naturales ,

• a partir de algunas de las observaciones más importantes, como la expansión del universo, donde la razón común r está definida por la constante de Hubble ,
• a algunas de las observaciones más pequeñas, como la desintegración de los átomos radiactivos de carbono-14, donde la relación común r se define por la vida media del carbono-14 .

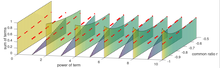
Aparte, la razón común r puede ser un número complejo como | r | e ^{i θ} donde | r | es el vector magnitud 's (o longitud), θ es el ángulo del vector (u orientación) en el plano complejo y i ² = -1. Con una proporción común | r | e ^{i θ} , la forma expandida de la serie geométrica es a + a | r | e ^{i θ} + a | r | ² e ^{i2 θ} + a | r | ³ e ^{i3 θ} + ... Modelando el ángulo θ como aumentando linealmente con el tiempo a la tasa de alguna frecuencia angular ω ₀ (en otras palabras, haciendo la sustitución θ = ω ₀ t ), la forma expandida de la serie geométrica se convierte en una + a | r | e ^{yo ω ₀ t} + a | r | ² e ^{i2 ω ₀ t} + a | r | ³ e ^{i3 ω ₀ t} + ..., donde el primer término es un vector de longitud a que no gira en absoluto, y todos los demás términos son vectores de diferentes longitudes que giran en armónicos de la frecuencia angular fundamental ω ₀ . La restricción | r | <1 es suficiente para coordinar este número infinito de vectores de diferentes longitudes, todos girando a diferentes velocidades para trazar un círculo, como se muestra en el video adyacente. Similar a cómo la serie de Taylor describe cómo cambiar los coeficientes para que la serie converja a una función suficientemente suave seleccionada por el usuario dentro de un rango, la serie de Fourier describe cómo cambiar los coeficientes (que también pueden ser números complejos para especificar los ángulos iniciales de vectores) para que la serie converja a una función periódica seleccionada por el usuario .

Suma

Fórmula de forma cerrada

Ofreciendo una perspectiva diferente de la conocida derivación algebraica dada en la sección adyacente, la siguiente es una derivación geométrica de la forma cerrada de la serie geométrica. Como resumen, esta derivación geométrica representa los términos de la serie geométrica como áreas de cuadrados superpuestos y el objetivo es transformar esos cuadrados superpuestos en un área no superpuesta de fácil cálculo. El punto de partida es la suma parcial S = r ^m + r ^{m + 1} + ... + r ^n-1 + r ⁿ cuando m <n y razón común r > 1. Cada término de la serie r ⁱ está representado por el área de un cuadrado superpuesto de área A _i que se puede transformar en un área en forma de L no superpuesta L _i = A _i - A _i-1 o, de manera equivalente, L _{i + 1} = A _{i + 1} - A _i . Por ser una serie geométrica, A _{i + 1} = r A _i . Por lo tanto, L _{i + 1} = A _{i + 1} - A _i = (r - 1) A _i , o A _i = L _{i + 1} / ( r - 1). En palabras, cada cuadrado se superpone, pero se puede transformar en un área en forma de L no superpuesta en el siguiente cuadrado más grande (siguiente potencia de r ) y se escala en 1 / ( r - 1) para que la transformación de un cuadrado superpuesto a no -El área en forma de L superpuesta mantiene la misma área. Por lo tanto, la suma S = A _m + A _{m + 1} + ... + A _n-1 + A _n = (L _{m + 1} + L _{m + 2} + ... + L _n + L _{n + 1} ) / ( r - 1). Observe que las áreas en forma de L no superpuestas desde el área en forma de L m + 1 hasta el área en forma de L n + 1 son una partición del cuadrado no superpuesto A _{n + 1} menos la muesca del cuadrado superior derecho A _m (porque hay no hay cuadrados más pequeños superpuestos para transformarlos en esa muesca del área A _m ). Por lo tanto, al sustituir A _i = r ⁱ y escalar todos los términos por el coeficiente a, se obtiene la serie geométrica general de forma cerrada S = ( r ^{n + 1} - r ^m ) a / ( r - 1) cuando m <n y r > 1. Aunque la prueba geométrica anterior supone r > 1, se puede demostrar que la misma fórmula de forma cerrada se aplica a cualquier valor de r con la posible excepción de r = 0 (dependiendo de cómo elija definir cero elevado a la potencia de cero ). Por ejemplo, para el caso de r = 1, S = (1 ^{n + 1} - 1 ^m ) a / (1 - 1) = 0 / 0. Sin embargo, la aplicación de la regla de L'Hôpital da como resultado S = (n + 1 - m ) a cuando r = 1. Para el caso de 0 <r <1, ​​comience con S = ( r ^{n + 1} - r ^m ) a / ( r - 1) cuando m <n, r > 1 y sea m = - ∞ y n = 0 entonces S = ar / ( r - 1) cuando r > 1. Dividir el numerador y el denominador por r da S = a / (1 - (1 / r )) cuando r > 1, que es equivalente a S = a / (1 - r ) cuando 0 < r <1 porque invertir r invierte el orden de la serie (de mayor a menor en lugar de menor a mayor) pero no cambia la suma. El rango 0 < r <1 se puede extender al rango -1 < r <1 aplicando la fórmula derivada, S = a / (1 - r ) cuando 0 < r <1, por separado a dos particiones de la serie geométrica: uno con potencias pares de r (que no puede ser negativo) y el otro con potencias impares de r (que puede ser negativo). La suma de ambas particiones es S = a / (1 - r ² ) + ar / (1 - r ² ) = a (1 + r ) / ((1 + r ) (1 - r )) = a / (1 - r ).

Porque , la suma de los primeros n +1 términos de una serie geométrica, hasta e incluyendo el término r ⁿ , es ${\ Displaystyle r \ neq 1}$

${\ Displaystyle a + ar + ar ^ {2} + ar ^ {3} + \ cdots + ar ^ {n} = \ sum _ {k = 0} ^ {n} ar ^ {k} = a \ left ( {\ frac {1-r ^ {n + 1}} {1-r}} \ derecha),}$

donde r es la razón común. Uno puede derivar esa fórmula de forma cerrada para la suma parcial, s , restando los muchos términos auto-similares de la siguiente manera:

${\ Displaystyle {\ begin {alineado} s = a \ + \ & ar \ + \ ar ^ {2} \ + \ ar ^ {3} \ + \ \ cdots \ + \ ar ^ {n}, \\ rs = \ & ar \ + \ ar ^ {2} \ + \ ar ^ {3} \ + \ \ cdots \ + \ ar ^ {n} \ + \ ar ^ {n + 1}, \\ s-rs = \ & a \ - \ ar ^ {n + 1}, \\ s (1-r) = \ & a (1-r ^ {n + 1}), \\ s = \ & a \ left ({\ frac {1-r ^ {n + 1}} {1-r}} \ right) \ quad {\ text {(if}} r \ neq 1 {\ text {)}}. \ end {alineado}}}$

A medida que n se acerca al infinito, el valor absoluto de r debe ser menor que uno para que la serie converja. La suma luego se convierte en

${\ Displaystyle a + ar + ar ^ {2} + ar ^ {3} + ar ^ {4} + \ cdots = \ sum _ {k = 0} ^ {\ infty} ar ^ {k} = {\ frac {a} {1-r}}, {\ text {para}} | r | <1.}$

Cuando a = 1 , esto se puede simplificar a

${\ Displaystyle 1 \, + \, r \, + \, r ^ {2} \, + \, r ^ {3} \, + \, \ cdots \; = \; {\ frac {1} {1 -r}}.}$

La fórmula también es válida para el complejo r , con la restricción correspondiente, el módulo de r es estrictamente menor que uno.

Aparte, la cuestión de si una serie infinita converge es fundamentalmente una cuestión de la distancia entre dos valores: dados suficientes términos, ¿el valor de la suma parcial se acerca arbitrariamente al valor al que se aproxima? En la derivación anterior de la forma cerrada de la serie geométrica, la interpretación de la distancia entre dos valores es la distancia entre sus ubicaciones en la recta numérica . Esa es la interpretación más común de la distancia entre dos valores. Sin embargo, la métrica p-ádica , que se ha convertido en una noción crítica en la teoría de números moderna , ofrece una definición de distancia tal que la serie geométrica 1 + 2 + 4 + 8 + ... con a = 1 y r = 2 en realidad converge a a / (1 - r ) = 1 / (1 - 2) = -1 aunque r está fuera del rango de convergencia típico | r | <1.

Prueba de convergencia

Podemos probar que la serie geométrica converge usando la fórmula de suma para una progresión geométrica :

${\ displaystyle {\ begin {alineado} 1 + r + r ^ {2} + r ^ {3} + \ cdots \ & = \ lim _ {n \ rightarrow \ infty} \ left (1 + r + r ^ { 2} + \ cdots + r ^ {n} \ right) \\ & = \ lim _ {n \ rightarrow \ infty} {\ frac {1-r ^ {n + 1}} {1-r}}. \ final {alineado}}}$

La segunda igualdad es verdadera porque si entonces como y ${\ Displaystyle | r | <1,}$${\ Displaystyle r ^ {n + 1} \ to 0}$${\ Displaystyle n \ to \ infty}$

${\ Displaystyle {\ begin {alineado} (1 + r + r ^ {2} + \ cdots + r ^ {n}) (1-r) & = ((1-r) + (rr ^ {2}) + (r ^ {2} -r ^ {3}) + ... + (r ^ {n} -r ^ {n + 1})) \\ & = (1 + (- r + r) + ( -r ^ {2} + r ^ {2}) + ... + (- r ^ {n} + r ^ {n}) - r ^ {n + 1}) \\ & = 1-r ^ { n + 1}. \ end {alineado}}}$

La convergencia de series geométricas también se puede demostrar reescribiendo la serie como una serie telescópica equivalente . Considere la función,

${\ Displaystyle g (K) = {\ frac {r ^ {K}} {1-r}}.}$

Tenga en cuenta que

${\ Displaystyle 1 = g (0) -g (1), \ quad r = g (1) -g (2), \ quad r ^ {2} = g (2) -g (3), \ ldots}$

Por lo tanto,

${\ Displaystyle S = 1 + r + r ^ {2} + r ^ {3} + \ cdots = (g (0) -g (1)) + (g (1) -g (2)) + (g (2) -g (3)) + \ cdots.}$

Si

${\ Displaystyle | r | <1}$

luego

${\ displaystyle g (K) \ longrightarrow 0 {\ text {as}} K \ a \ infty.}$

Entonces S converge a

${\ displaystyle g (0) = {\ frac {1} {1-r}}.}$

Tasa de convergencia

La suma acumulada de funciones dentro del rango -1 < r <-0.5 cuando se agregan los primeros 51 términos de la serie geométrica 1 + r + r ² + r ³ + ... La magnitud de la pendiente en r = -1 aumenta muy gradualmente con cada término agregado. La serie geométrica 1 / (1 - r ) es la línea discontinua roja.

Como se muestra en las demostraciones anteriores, la forma cerrada de la suma parcial de la serie geométrica hasta e incluyendo la n -ésima potencia de r es a (1 - r ^{n +1} ) / (1 - r ) para cualquier valor de r , y la forma cerrada de la serie geométrica es la suma completa a / (1 - r ) dentro del rango | r | <1.

Si la razón común está dentro del rango 0 < r <1, entonces la suma parcial a (1 - r ^{n +1} ) / (1 - r ) aumenta con cada término agregado y eventualmente se encuentra dentro de algún pequeño error, E , razón de la suma completa a / (1 - r ). Resolviendo n en ese umbral de error,

${\ Displaystyle {\ begin {alineado} a \ left ({\ frac {1-r ^ {n + 1}} {1-r}} \ right) & \ geq a \ left ({\ frac {1-E } {1-r}} \ right), \\ 1-r ^ {n + 1} & \ geq 1-E, \\ r ^ {n + 1} & \ leq E, \\\ ln (r ^ {n + 1}) & \ leq \ ln (E), \\ (n + 1) \ ln (r) & \ leq \ ln (E), \\ n + 1 & \ geq \ left \ lceil {\ frac {\ ln (E)} {\ ln (r)}} \ right \ rceil, \ end {alineado}}}$

donde 0 < r <1, la operación de techo restringe n a números enteros, y dividir ambos lados por el logaritmo natural de r invierte la desigualdad porque es negativa. El resultado n +1 es el número de términos de suma parcial necesarios para obtener dentro de aE / (1 - r ) de la suma completa a / (1 - r ). Por ejemplo, para obtener dentro del 1% de la suma total a / (1 - r ) en r = 0.1, solo 2 (= ln ( E ) / ln ( r ) = ln (0.01) / ln (0.1)) términos de la Se necesita suma parcial. Sin embargo, en r = 0.9, 44 (= ln (0.01) / ln (0.9)) los términos de la suma parcial son necesarios para llegar al 1% de la suma total a / (1 - r ). ${\ Displaystyle \ lceil \ rceil}$

Si la razón común está dentro del rango -1 < r <0, entonces la serie geométrica es una serie alterna pero se puede convertir a la forma de una serie geométrica no alterna combinando pares de términos y luego analizando la tasa de convergencia usando el mismo enfoque que se muestra para el rango de razón común 0 < r <1. Específicamente, la suma parcial

s = a + ar + ar ² + ar ³ + ar ⁴ + ar ⁵ + ... + ar ^{n -1} + ar ⁿ dentro del rango -1 < r <0 es equivalente a

s = a - ap + ap ² - ap ³ + ap ⁴ - ap ⁵ + ... + ap ^{n -1} - ap ⁿ con una n impar, con la sustitución de p = - r , y dentro del rango 0 < p <1,

s = ( a - ap ) + ( ap ² - ap ³ ) + ( ap ⁴ - ap ⁵ ) + ... + ( ap ^{n -1} - ap ⁿ ) con términos adyacentes y con signos diferentes emparejados,

s = a (1 - p ) + a (1 - p ) p ² + a (1 - p ) p ⁴ + ... + a (1 - p ) p ^{2 ( n -1) / 2} con a (1 - p ) factorizado de cada término,

s = a (1 - p ) + a (1 - p ) p ² + a (1 - p ) p ⁴ + ... + a (1 - p ) p ^{2 m} con la sustitución m = ( n - 1) / 2 que es un número entero dada la restricción de que n es impar,

que ahora tiene la forma de los primeros m términos de una serie geométrica con coeficiente a (1 - p ) y con razón común p ² . Por lo tanto, la forma cerrada de la suma parcial es a (1 - p ) (1 - p ^{2 ( m +1)} ) / (1 - p ² ) que aumenta con cada término agregado y eventualmente se encuentra dentro de algún pequeño error, E , razón de la suma total a (1 - p ) / (1 - p ² ). Como antes, resolviendo para m en ese umbral de error,

${\ Displaystyle {\ begin {alineado} a (1-p) \ left ({\ frac {1-p ^ {2m + 2}} {1-p ^ {2}}} \ right) & \ geq a ( 1-p) \ left ({\ frac {1-E} {1-p ^ {2}}} \ right), \\ 1-p ^ {2m + 2} & \ geq 1-E, \\ p ^ {2m + 2} & \ leq E, \\\ ln (p ^ {2m + 2}) & \ leq \ ln (E), \\ (2m + 2) \ ln (p) & \ leq \ ln (E), \\ m + 1 & \ geq \ left \ lceil {\ frac {\ ln (E)} {2 \ ln (p)}} \ right \ rceil, \\ m + 1 & \ geq \ left \ lceil {\ frac {\ ln (E)} {2 \ ln (-r)}} \ right \ rceil, \ end {alineado}}}$

donde 0 < p <1 o equivalentemente -1 < r <0, y el resultado m +1 es el número de pares de términos de suma parcial necesarios para obtener dentro de a (1 - p ) E / (1 - p ² ) del suma completa a (1 - p ) / (1 - p ² ). Por ejemplo, para obtener dentro del 1% de la suma total a (1 - p ) / (1 - p ² ) en p = 0.1 o equivalentemente r = -0.1, solo 1 (= ln ( E ) / (2 ln ( p ) ) = ln (0.01) / (2 ln (0.1)) par de términos de la suma parcial son necesarios. Sin embargo, en p = 0.9 o equivalentemente r = -0.9, 22 (= ln (0.01) / (2 ln (0.9) )) Se necesitan pares de términos de la suma parcial para obtener dentro del 1% de la suma total a (1 - p ) / (1 - p ² ). Comparación de la tasa de convergencia para valores positivos y negativos de r , n + 1 (el número de términos requeridos para alcanzar el umbral de error para algún r positivo ) es siempre dos veces mayor que m + 1 (el número de pares de términos requeridos para alcanzar el umbral de error para el negativo de ese r ) pero el m + 1 se refiere a pares de términos en lugar de términos simples. Por lo tanto, la tasa de convergencia es simétrica alrededor de r = 0, lo que puede ser una sorpresa dada la asimetría de a / (1 - r ). Una perspectiva que ayuda a explicar esta tasa de simetría de convergencia es que en el lado r > 0, cada término agregado de la suma parcial hace una con contribución a la suma infinita en r = 1 mientras que en el lado r <0 cada término agregado hace una contribución finita a la pendiente infinita en r = -1.

Por otro lado, este tipo de análisis de tasa de convergencia es particularmente útil cuando se calcula el número de términos de la serie de Taylor necesarios para aproximar adecuadamente alguna función suficientemente suave seleccionada por el usuario o cuando se calcula el número de términos de la serie de Fourier necesarios para aproximar adecuadamente algunos términos del usuario. función periódica seleccionada.

Perspectivas históricas

Zenón de Elea (c.495 - c.430 aC)

Hace 2.500 años, los matemáticos griegos tenían problemas para caminar de un lugar a otro. Físicamente, pudieron caminar tan bien como nosotros hoy, quizás mejor. Sin embargo, lógicamente pensaban que una lista infinitamente larga de números mayores que cero sumaba infinito. Por lo tanto, fue una paradoja cuando Zenón de Elea señaló que para caminar de un lugar a otro, primero tienes que caminar la mitad de la distancia, luego tienes que caminar la mitad de la distancia restante, y luego tienes que caminar la mitad de la distancia. de esa distancia restante, y continúas dividiendo a la mitad las distancias restantes un número infinito de veces porque no importa cuán pequeña sea la distancia restante, todavía tienes que caminar la primera mitad. Por lo tanto, Zenón de Elea transformó una distancia corta en una lista infinitamente larga de distancias restantes reducidas a la mitad, todas las cuales son mayores que cero. Y ese era el problema: ¿cómo puede una distancia ser corta cuando se mide directamente y también infinita cuando se suma en su lista infinita de residuos reducidos a la mitad? La paradoja reveló que algo andaba mal con la suposición de que una lista infinitamente larga de números mayores que cero sumaban infinito.

Euclides de Alejandría (c. 300 a. C.)

Elements of Geometry, Libro IX, Proposición 35. "Si hay una multitud cualquiera de números continuamente proporcionales, e igual al primero se resta del segundo y el último, entonces como el exceso del segundo al primero, entonces el exceso del último será para todos los que le precedieron ".

Para el mismo caso de razón común r > 1, hay otras demostraciones geométricas de la forma cerrada de suma parcial de la serie geométrica. Uno que representa términos como áreas en lugar de longitudes de segmentos de línea se resume, como se muestra en la figura anterior, en tres pasos: (ARRIBA) Representa los términos de una serie geométrica como las áreas de triángulos similares superpuestos. (MEDIO) Del triángulo más grande al más pequeño, elimine la parte del área izquierda superpuesta (1 / r ) de la parte del área derecha no superpuesta (1-1 / r = ( r -1) / r ) y escale ese trapezoide superpuesto por r / ( r -1) por lo que su área es la misma que el área del triángulo superpuesto original. (ABAJO) Observe que el área del trapezoide agregado es el área de un triángulo grande menos el área de un triángulo pequeño vacío en la punta izquierda del triángulo grande. El triángulo grande es exactamente el triángulo superpuesto más grande escalado por r / ( r -1). El pequeño triángulo vacío comenzó como un pero esa área se transformó en un trapezoide escalado no superpuesto dejando una parte del área izquierda vacía (1 / r ). Sin embargo, ese triángulo vacío de área a / r también debe ser escalado por r / ( r -1) para que su pendiente coincida con la pendiente de todos los trapezoides escalados no superpuestos. Por lo tanto, S _n = área del triángulo grande - área del triángulo pequeño vacío = ar ^{n + 1} / ( r -1) - a / ( r -1) = a ( r ^{n + 1} -1) / ( r -1) .

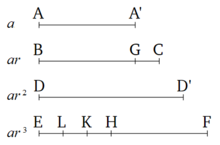
Euclides Elements of Geometry Book IX, Proposición 35, prueba (de la proposición en el título del diagrama adyacente):

Sea AA ', BC, DD', EF cualquier multitud de números continuamente proporcionales, comenzando por el menor AA '. Y supongamos que BG y FH, cada uno igual a AA ', se han restado de BC y EF. Digo que así como GC es para AA ', EH es para AA', BC, DD '.

Pues hagamos que FK sea igual a BC y FL a DD '. Y como FK es igual a BC, de la cual FH es igual a BG, el resto HK es, por tanto, igual al resto GC. Y como EF es a DD ', entonces DD' a BC y BC a AA '[Prop. 7.13], y DD 'igual a FL, y BC a FK, y AA' a FH, así como EF es a FL, entonces LF a FK y FK a FH. Por separación, como EL a LF, entonces LK a FK y KH a FH [Props. 7,11, 7,13]. Y así como uno de los principales es uno de los siguientes, así (la suma de) todos los principales a (la suma de) todos los siguientes [Prop. 7.12]. Así, como KH es para FH, entonces EL, LK, KH para LF, FK, HF. Y KH es igual a CG, y FH a AA ', y LF, FK, HF a DD', BC, AA '. Así, así como CG es para AA ', EH para DD', BC, AA '. Así, como el exceso del segundo es para el primero, así es el exceso del último para todos los anteriores. Precisamente lo que se le pedía que mostrara.

La concisión de las proposiciones y pruebas de Euclides puede haber sido una necesidad. Tal como está, los Elementos de Geometría son más de 500 páginas de proposiciones y pruebas. Hacer copias de este popular libro de texto requirió mucho trabajo, dado que la imprenta no se inventó hasta 1440. Y la popularidad del libro duró mucho tiempo: como se indica en la introducción citada a una traducción al inglés, Elements of Geometry "tiene la distinción de ser el el libro de texto matemático de uso continuo más antiguo del mundo ". Entonces, ser muy conciso era ser muy práctico. La prueba de la Proposición 35 en el Libro IX podría haber sido aún más compacta si Euclides hubiera podido evitar de alguna manera igualar explícitamente longitudes de segmentos de línea específicos de diferentes términos en la serie. Por ejemplo, la notación contemporánea para series geométricas (es decir, a + ar + ar ² + ar ³ + ... + ar ⁿ ) no etiqueta porciones específicas de términos que son iguales entre sí.

También en la introducción citada, el editor comenta:

La mayoría de los teoremas que aparecen en los Elementos no fueron descubiertos por el propio Euclides, sino que fueron obra de matemáticos griegos anteriores como Pitágoras (y su escuela), Hipócrates de Quíos, Teteto de Atenas y Eudoxo de Cnidos. Sin embargo, a Euclides se le atribuye generalmente el haber ordenado estos teoremas de una manera lógica, para demostrar (es cierto, no siempre con el rigor exigido por las matemáticas modernas) que necesariamente se siguen de cinco axiomas simples. A Euclides también se le atribuye haber ideado una serie de demostraciones particularmente ingeniosas de teoremas previamente descubiertos (por ejemplo, el Teorema 48 en el Libro 1).

Para ayudar a traducir la proposición y la prueba a una forma que use la notación actual, hay un par de modificaciones en el diagrama. Primero, las cuatro longitudes de línea horizontal que representan los valores de los primeros cuatro términos de una serie geométrica ahora están etiquetadas a, ar, ar ² , ar ³ en el margen izquierdo del diagrama. En segundo lugar, las nuevas etiquetas A 'y D' están ahora en la primera y la tercera línea para que todos los nombres de los segmentos de línea del diagrama especifiquen consistentemente el punto de inicio y el punto final del segmento.

Aquí hay una interpretación frase por frase de la proposición:

De manera similar, aquí hay una interpretación oración por oración de la prueba:

Arquímedes de Siracusa (c.287 - c.212 aC)

Disección de Arquímedes de un segmento parabólico en infinitos triángulos

Arquímedes usó la suma de una serie geométrica para calcular el área encerrada por una parábola y una línea recta. Su método consistía en diseccionar el área en un número infinito de triángulos.

El teorema de Arquímedes establece que el área total bajo la parábola es 4/3 del área del triángulo azul.

Arquímedes determinó que cada triángulo verde tiene 1/8 del área del triángulo azul, cada triángulo amarillo tiene 1/8 del área de un triángulo verde, y así sucesivamente.

Suponiendo que el triángulo azul tiene un área 1, el área total es una suma infinita:

${\ Displaystyle 1 \, + \, 2 \ left ({\ frac {1} {8}} \ right) \, + \, 4 \ left ({\ frac {1} {8}} \ right) ^ { 2} \, + \, 8 \ left ({\ frac {1} {8}} \ right) ^ {3} \, + \, \ cdots.}$

El primer término representa el área del triángulo azul, el segundo término las áreas de los dos triángulos verdes, el tercer término las áreas de los cuatro triángulos amarillos, y así sucesivamente. Simplificar las fracciones da

${\ Displaystyle 1 \, + \, {\ frac {1} {4}} \, + \, {\ frac {1} {16}} \, + \, {\ frac {1} {64}} \ , + \, \ cdots.}$

Esta es una serie geométrica con una relación común 1/4 y la parte fraccionaria es igual a

${\ Displaystyle \ sum _ {n = 0} ^ {\ infty} 4 ^ {- n} = 1 + 4 ^ {- 1} +4 ^ {- 2} +4 ^ {- 3} + \ cdots = { 4 \ sobre 3}.}$

La suma es

${\ Displaystyle {\ frac {1} {1-r}} \; = \; {\ frac {1} {1 - {\ frac {1} {4}}}} \; = \; {\ frac { 4} {3}}.}$

Este cálculo utiliza el método de agotamiento , una versión temprana de integración . Usando cálculo , la misma área se puede encontrar mediante una integral definida .

Nicole Oresme (hacia 1323-1382)

Un diagrama bidimensional de series geométricas que Nicole Oresme utilizó para determinar que la serie infinita 1/2 + 2/4 + 3/8 + 4/16 + 5/32 + 6/64 + 7/128 + ... converge en 2.

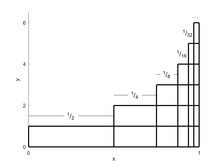
Entre sus intuiciones sobre las series infinitas, además de su prueba elegantemente simple de la divergencia de la serie armónica, Nicole Oresme demostró que la serie 1/2 + 2/4 + 3/8 + 4/16 + 5/32 + 6 / 64 + 7/128 + ... converge a 2. Su diagrama para su demostración geométrica, similar al diagrama adyacente, muestra una serie geométrica bidimensional. La primera dimensión es horizontal, en la fila inferior que muestra la serie geométrica S = 1/2 + 1/4 + 1/8 + 1/16 + ..., que es la serie geométrica con coeficiente a = 1/2 y común relación r = 1/2 que converge a S = a / (1- r ) = (1/2) / (1-1 / 2) = 1. La segunda dimensión es vertical, donde la fila inferior es un nuevo coeficiente a _{T es} igual a S y cada fila subsiguiente por encima de ella se escala con la misma razón común r = 1/2, lo que hace que otra serie geométrica T = 1 + 1/2 + 1/4 + 1/8 + ..., que es la serie geométrica con coeficiente a _T = S = 1 y razón común r = 1/2 que converge a T = a _T / (1- r ) = S / (1- r ) = a / (1- r ) / (1 - r ) = (1/2) / (1-1 / 2) / (1-1 / 2) = 2.

Aunque es difícil de visualizar más allá de las tres dimensiones, la percepción de Oresme se generaliza a cualquier dimensión d . El uso de la suma de la dimensión d −1 de la serie geométrica como el coeficiente a en la dimensión d de la serie geométrica da como resultado una serie geométrica d- dimensional que converge a S ^d / a = 1 / (1- r ) ^d dentro de la rango | r | <1. El triángulo de Pascal y la división larga revelan los coeficientes de estas series geométricas multidimensionales, donde la forma cerrada es válida solo dentro del rango | r | <1.

${\ Displaystyle {\ begin {matrix} {\ text {1}} \\ {\ text {1}} \ quad {\ text {1}} \\ {\ text {1}} \ quad {\ text {2 }} \ quad {\ text {1}} \\ {\ text {1}} \ quad {\ text {3}} \ quad {\ text {3}} \ quad {\ text {1}} \\ { \ text {1}} \ quad {\ text {4}} \ quad {\ text {6}} \ quad {\ text {4}} \ quad {\ text {1}} \ end {matriz}}}$

${\ displaystyle {\ begin {alineado} & d \ quad S ^ {d} / a \ {\ text {(forma cerrada)}} \ quad && S ^ {d} / a \ {\ text {(forma expandida)}} \\ & 1 \ quad 1 / (1-r) \ quad && 1 + r + r ^ {2} + r ^ {3} + r ^ {4} + \ cdots \\ & 2 \ quad 1 / (1-r) ^ {2} \ quad && 1 + 2r + 3r ^ {2} + 4r ^ {3} + 5r ^ {4} + \ cdots \\ & 3 \ quad 1 / (1-r) ^ {3} \ quad && 1 + 3r + 6r ^ {2} + 10r ^ {3} + 15r ^ {4} + \ cdots \\ & 4 \ quad 1 / (1-r) ^ {4} \ quad && 1 + 4r + 10r ^ {2} + 20r ^ {3} + 35r ^ {4} + \ cdots \\\ end {alineado}}}$

Tenga en cuenta que, como alternativa a la división larga, también es posible calcular los coeficientes de la serie geométrica d- dimensional integrando los coeficientes de dimensión d -1. Este mapeo desde la división por 1- r en el dominio de la suma de la serie de potencias hasta la integración en el dominio del coeficiente de la serie de potencias es una forma discreta del mapeo realizado por la transformada de Laplace . El profesor del MIT Arthur Mattuck muestra cómo derivar la transformada de Laplace a partir de la serie de potencias en este video de conferencia, donde la serie de potencia es un mapeo entre coeficientes discretos y una suma y la transformada de Laplace es un mapeo entre pesos continuos y una integral.

Las formas cerradas de S ^d / a están relacionadas pero no son iguales a las derivadas de S = f ( r ) = 1 / (1- r ). Como se muestra en la siguiente tabla, la relación es S ^{k +1} = f ^{( k )} ( r ) / k !, Donde f ^{( k )} ( r ) denota la k- ^ésima derivada de f ( r ) = 1 / (1- r ) y la forma cerrada es válida solo dentro del rango | r | <1.

${\ Displaystyle {\ begin {alineado} & k \ quad f ^ {(k)} (r) / a \ {\ text {(forma cerrada)}} \ quad && f ^ {(k)} (r) / a \ {\ text {(formulario de generador)}} \\ & 0 \ quad 1 / (1-r) \ quad && \ sum _ {j = 0} ^ {\ infty} r ^ {j} \\ & 1 \ quad 1! / (1-r) ^ {2} \ quad && \ sum _ {j = 1} ^ {\ infty} jr ^ {j-1} \\ & 2 \ quad 2! / (1-r) ^ {3} \ quad && \ sum _ {j = 2} ^ {\ infty} j (j-1) r ^ {j-2} \\ & 3 \ quad 3! / (1-r) ^ {4} \ quad && \ suma _ {j = 3} ^ {\ infty} j (j-1) (j-2) r ^ {j-3} \\ & 4 \ quad 4! / (1-r) ^ {5} \ quad && \ sum _ {j = 4} ^ {\ infty} j (j-1) (j-2) (j-3) r ^ {j-4} \\\ end {alineado}}}$

Aplicaciones

Decimales repetidos

Se puede pensar en un decimal periódico como una serie geométrica cuya razón común es una potencia de 1/10. Por ejemplo:

${\ Displaystyle 0,7777 \ ldots \; = \; {\ frac {7} {10}} \, + \, {\ frac {7} {100}} \, + \, {\ frac {7} {1000} } \, + \, {\ frac {7} {10000}} \, + \, \ cdots.}$

La fórmula para la suma de una serie geométrica se puede utilizar para convertir el decimal a una fracción,

${\ Displaystyle 0.7777 \ ldots \; = \; {\ frac {a} {1-r}} \; = \; {\ frac {7/10} {1-1 / 10}} \; = \; { \ frac {7/10} {9/10}} \; = \; {\ frac {7} {9}}.}$

La fórmula funciona no solo para una sola figura repetida, sino también para un grupo repetido de figuras. Por ejemplo:

${\ displaystyle 0.123412341234 \ ldots \; = \; {\ frac {a} {1-r}} \; = \; {\ frac {1234/10000} {1-1 / 10000}} \; = \; { \ frac {1234/10000} {9999/10000}} \; = \; {\ frac {1234} {9999}}.}$

Tenga en cuenta que cada serie de decimales consecutivos repetidos se puede simplificar convenientemente con lo siguiente:

${\ Displaystyle 0.09090909 \ ldots \; = \; {\ frac {09} {99}} \; = \; {\ frac {1} {11}}.}$

${\ displaystyle 0.143814381438 \ ldots \; = \; {\ frac {1438} {9999}}.}$

${\ Displaystyle 0.9999 \ ldots \; = \; {\ frac {9} {9}} \; = \; 1.}$

Es decir, un decimal periódico con longitud de repetición n es igual al cociente de la parte repetida (como un número entero) y 10 ⁿ - 1 .

Ciencias económicas

En economía , las series geométricas se utilizan para representar el valor presente de una anualidad (una suma de dinero a pagar en intervalos regulares).

Por ejemplo, suponga que se realizará un pago de $ 100 al propietario de la anualidad una vez al año (al final del año) a perpetuidad . Recibir $ 100 dentro de un año vale menos que $ 100 inmediatos, porque uno no puede invertir el dinero hasta que lo reciba. En particular, el valor presente de $ 100 un año en el futuro es $ 100 / (1 +  ), donde es la tasa de interés anual. ${\ Displaystyle I}$${\ Displaystyle I}$

De manera similar, un pago de $ 100 dos años en el futuro tiene un valor presente de $ 100 / (1 +  ) ² (al cuadrado porque los intereses de dos años se pierden al no recibir el dinero en este momento). Por lo tanto, el valor presente de recibir $ 100 por año a perpetuidad es ${\ Displaystyle I}$

${\ Displaystyle \ sum _ {n = 1} ^ {\ infty} {\ frac {\ $ 100} {(1 + I) ^ {n}}},}$

que es la serie infinita:

${\ Displaystyle {\ frac {\ $ 100} {(1 + I)}} \, + \, {\ frac {\ $ 100} {(1 + I) ^ {2}}} \, + \, {\ frac {\ $ 100} {(1 + I) ^ {3}}} \, + \, {\ frac {\ $ 100} {(1 + I) ^ {4}}} \, + \, \ cdots.}$

Ésta es una serie geométrica con una relación común 1 / (1 +  ). La suma es el primer término dividido por (uno menos la razón común): ${\ Displaystyle I}$

${\ Displaystyle {\ frac {\ $ 100 / (1 + I)} {1-1 / (1 + I)}} \; = \; {\ frac {\ $ 100} {I}}.}$

Por ejemplo, si la tasa de interés anual es del 10% (  = 0,10), entonces toda la anualidad tiene un valor presente de $ 100 / 0,10 = $ 1000. ${\ Displaystyle I}$

Este tipo de cálculo se utiliza para calcular la TAE de un préstamo (como un préstamo hipotecario ). También se puede utilizar para estimar el valor actual de los esperados dividendos de acciones , o el valor terminal de la seguridad .

Geometría fractal

El interior del copo de nieve de Koch es una unión de infinitos triángulos.

En el estudio de los fractales , las series geométricas a menudo surgen como el perímetro , el área o el volumen de una figura auto-similar .

Por ejemplo, el área dentro del copo de nieve de Koch se puede describir como la unión de infinitos triángulos equiláteros (ver figura). Cada lado del triángulo verde tiene exactamente 1/3 del tamaño de un lado del triángulo azul grande y, por lo tanto, tiene exactamente 1/9 del área. De manera similar, cada triángulo amarillo tiene 1/9 del área de un triángulo verde, y así sucesivamente. Tomando el triángulo azul como unidad de área, el área total del copo de nieve es

${\ Displaystyle 1 \, + \, 3 \ left ({\ frac {1} {9}} \ right) \, + \, 12 \ left ({\ frac {1} {9}} \ right) ^ { 2} \, + \, 48 \ left ({\ frac {1} {9}} \ right) ^ {3} \, + \, \ cdots.}$

El primer término de esta serie representa el área del triángulo azul, el segundo término el área total de los tres triángulos verdes, el tercer término el área total de los doce triángulos amarillos, y así sucesivamente. Excluyendo el 1 inicial, esta serie es geométrica con una relación constante r  = 4/9. El primer término de la serie geométrica es a  = 3 (1/9) = 1/3, por lo que la suma es

${\ Displaystyle 1 \, + \, {\ frac {a} {1-r}} \; = \; 1 \, + \, {\ frac {\ frac {1} {3}} {1 - {\ frac {4} {9}}}} \; = \; {\ frac {8} {5}}.}$

Por lo tanto, el copo de nieve de Koch tiene 8/5 del área del triángulo base.

Serie de potencia geométrica

La fórmula de una serie geométrica

${\ Displaystyle {\ frac {1} {1-x}} = 1 + x + x ^ {2} + x ^ {3} + x ^ {4} + \ cdots}$

se puede interpretar como una serie de potencias en el sentido del teorema de Taylor , convergiendo donde . A partir de esto, se puede extrapolar para obtener otras series de potencias. Por ejemplo, ${\ Displaystyle | x | <1}$

${\ Displaystyle {\ begin {alineado} \ tan ^ {- 1} (x) & = \ int {\ frac {dx} {1 + x ^ {2}}} \\ & = \ int {\ frac {dx } {1 - (- x ^ {2})}} \\ & = \ int \ left (1+ \ left (-x ^ {2} \ right) + \ left (-x ^ {2} \ right) ^ {2} + \ left (-x ^ {2} \ right) ^ {3} + \ cdots \ right) dx \\ & = \ int \ left (1-x ^ {2} + x ^ {4} -x ^ {6} + \ cdots \ right) dx \\ & = x - {\ frac {x ^ {3}} {3}} + {\ frac {x ^ {5}} {5}} - { \ frac {x ^ {7}} {7}} + \ cdots \\ & = \ sum _ {n = 0} ^ {\ infty} {\ frac {(-1) ^ {n}} {2n + 1 }} x ^ {2n + 1}. \ end {alineado}}}$

Ver también

• 0.999 ...  - Expansión decimal alternativa del número 1
• Asíntota  : límite de la recta tangente en un punto que tiende al infinito
• Serie geométrica divergente
• Función hipergeométrica generalizada
• Progresión geométrica
• Serie Neumann
• Prueba de razón
• Prueba de raíz
• Serie (matemáticas)  - Suma infinita
• Serie aritmética

Serie geométrica específica

• Serie de Grandi: la  suma infinita de términos alternos 1 y -1: 1 - 1 + 1 - 1 + ⋯
• 1 + 2 + 4 + 8 + ⋯  - Serie infinita
• 1-2 + 4-8 + ⋯
• 1/2 + 1/4 + 1/8 + 1/16 + ⋯
• 1/2 - 1/4 + 1/8 - 1/16 + ⋯
• 1/4 + 1/16 + 1/64 + 1/256 + ⋯
• Una serie geométrica es una serie unitaria (la suma de la serie converge en uno) si y solo si | r | <1 y a + r = 1 (equivalente a la forma más familiar S = a / (1 - r ) = 1 cuando | r | <1). Por lo tanto, una serie alterna también es una serie unitaria cuando -1 < r <0 y a + r = 1 (por ejemplo, coeficiente a = 1,7 y razón común r = -0,7).
• Los términos de una serie geométrica también son los términos de una secuencia de Fibonacci generalizada (F _n = F _n-1 + F _n-2 pero sin requerir F ₀ = 0 y F ₁ = 1) cuando una razón común r de una serie geométrica satisface el restricción 1 + r = r ² , que de acuerdo con la fórmula cuadrática es cuando la razón común r es igual a la razón áurea (es decir, la razón común r = (1 ± √5) / 2).
• Las series solamente geométricas que es una serie unidad y también tiene términos de una generalizada secuencia de Fibonacci tiene la proporción de oro como su coeficiente de una y el conjugado proporción de oro como su razón común r (es decir, un = (1 + √5) / 2 y r = (1 - √5) / 2). Es una serie unitaria porque a + r = 1 y | r | <1, es una secuencia de Fibonacci generalizada porque 1 + r = r ² , y es una serie alterna porque r <0.

Notas

Referencias

enlaces externos

• "Progresión geométrica" , Enciclopedia de matemáticas , EMS Press , 2001 [1994]
• Weisstein, Eric W. "Serie geométrica" . MathWorld .
• Serie geométrica en PlanetMath .
• Peppard, Kim. "Tutorial de álgebra universitaria sobre secuencias y series geométricas" . Universidad West Texas A&M.
• Casselman, Bill. "Una interpretación geométrica de la serie geométrica" . Archivado desde el original (Applet) el 29 de septiembre de 2007.
• "Serie geométrica" de Michael Schreiber, Wolfram Demonstrations Project , 2007.