Heyting álgebra - Heyting algebra

En matemáticas , un álgebra de Heyting (también conocida como álgebra pseudo-booleana ) es una red acotada (con operaciones de unión y encuentro escritas ∨ y ∧ y con el elemento mínimo 0 y el elemento mayor 1) equipado con una operación binaria a → b de implicación tal que ( c ∧ a ) ≤ b es equivalente ac ≤ ( a → b ). Desde un punto de vista lógico, A → B es según esta definición la proposición más débil para la cual modus ponens , la regla de inferencia A → B , A ⊢ B , es sólida. Como las álgebras de Boole , las álgebras de Heyting forman una variedad axiomatizable con un número finito de ecuaciones. Las álgebras de Heyting fueron introducidas por Arend Heyting  ( 1930 ) para formalizar la lógica intuicionista .

Como retículas, las álgebras de Heyting son distributivas . Cada álgebra booleana es un álgebra de Heyting cuando a → b se define como de costumbre como ¬ a ∨ b , al igual que todo retículo distributivo completo que satisface una ley distributiva infinita unilateral cuando a → b se toma como el supremo del conjunto de todos c para lo cual c ∧ a ≤ b . En el caso finito, cada retícula distributiva no vacía, en particular cada cadena finita no vacía , es automáticamente completa y completamente distributiva y, por tanto, es un álgebra de Heyting.

De la definición se deduce que 1 ≤ 0 → a , correspondiente a la intuición de que cualquier proposición a está implícita en una contradicción 0. Aunque la operación de negación ¬ a no forma parte de la definición, se puede definir como a → 0. El intuitivo El contenido de ¬ a es la proposición de que asumir a conduciría a una contradicción. La definición implica que a ∧ ¬ a = 0. Puede demostrarse además que a ≤ ¬¬ a , aunque lo contrario, ¬¬ a ≤ a , no es cierto en general, es decir, la eliminación de la doble negación no se cumple en general. en un álgebra de Heyting.

Las álgebras de Heyting generalizan las álgebras booleanas en el sentido de que una álgebra de Heyting que satisface a ∨ ¬ a = 1 ( centro excluido ), equivalentemente ¬¬ a = a ( eliminación de doble negación ), es un álgebra booleana. Los elementos de un álgebra de Heyting H de la forma ¬ a comprenden una red booleana, pero en general no es una subálgebra de H (ver más abajo ).

Las álgebras de Heyting sirven como modelos algebraicos de la lógica intuicionista proposicional de la misma manera que las álgebras booleanas modelan la lógica clásica proposicional . La lógica interna de un topos elemental se basa en el álgebra de Heyting de subobjetos del objeto terminal 1 ordenados por inclusión, equivalentemente los morfismos de 1 al clasificador de subobjetos Ω.

Los conjuntos abiertos de cualquier espacio topológico forman un álgebra de Heyting completa . Las álgebras de Heyting completas se convierten así en un objeto central de estudio en la topología sin sentido .

Cada álgebra de Heyting cuyo conjunto de elementos no mayores tiene un elemento mayor (y forma otra álgebra de Heyting) es subdirectamente irreductible , por lo que cada álgebra de Heyting puede hacerse subdirectamente irreductible mediante la unión de un nuevo elemento mayor. De ello se deduce que incluso entre las álgebras finitas de Heyting existen infinitos que son subdirectamente irreductibles, de los cuales no hay dos que tengan la misma teoría ecuacional. Por tanto, ningún conjunto finito de álgebras de Heyting finitas puede proporcionar todos los contraejemplos de las no leyes del álgebra de Heyting. Esto está en marcado contraste con las álgebras de Boole, cuya única subdirección irreductible es la de dos elementos, que por sí sola, por lo tanto, es suficiente para todos los contraejemplos de las no leyes del álgebra de Boole, la base del método de decisión de tabla de verdad simple . Sin embargo, es decidible si una ecuación es válida para todas las álgebras de Heyting.

Las álgebras de Heyting se denominan con menos frecuencia álgebras pseudo-booleanas , o incluso retículas de Brouwer , aunque este último término puede denotar la definición dual o tener un significado un poco más general.

Definicion formal

Un álgebra de Heyting H es una red acotada tal que para todo a y b en H hay un elemento mayor x de H tal que

${\ Displaystyle a \ wedge x \ leq b.}$

Este elemento es el pseudo-complemento relativo de a con respecto a b , y se denota a → b . Escribimos 1 y 0 para el elemento más grande y más pequeño de H , respectivamente.

En cualquier álgebra de Heyting, se define el pseudo-complemento ¬ a de cualquier elemento a estableciendo ¬ a = ( a → 0). Por definición, y ¬ a es el elemento más grande que tiene esta propiedad. Sin embargo, en general no es cierto que , por lo tanto, ¬ sea solo un pseudocomplemento, no un complemento verdadero , como sería el caso en un álgebra booleana. ${\ Displaystyle a \ wedge \ lnot a = 0}$${\ Displaystyle a \ vee \ lnot a = 1}$

Un álgebra de Heyting completa es un álgebra de Heyting que es una celosía completa .

Una subálgebra de un álgebra de Heyting H es un subconjunto H ₁ de H que contiene 0 y 1 y se cierra bajo las operaciones ∧, ∨ y →. De ello se deduce que también está cerrado bajo ¬. Una subálgebra se convierte en un álgebra de Heyting mediante las operaciones inducidas.

Definiciones alternativas

Definición teórica de categorías

Un álgebra de Heyting es una red acotada que tiene todos los objetos exponenciales . ${\ Displaystyle H}$

La celosía se considera como una categoría donde se reúne , es el producto . La condición exponencial significa que para cualquier objeto y en una exponencial existe de forma única como un objeto en . ${\ Displaystyle H}$${\ Displaystyle \ wedge}$${\ Displaystyle Y}$${\ Displaystyle Z}$${\ Displaystyle H}$${\ Displaystyle Z ^ {Y}}$${\ Displaystyle H}$

Una implicación de Heyting (a menudo escrita usando o para evitar confusiones como el uso de para indicar un funtor ) es solo una exponencial: es una notación alternativa para . De la definición de exponenciales, tenemos que la implicación ( ) es un adjunto a la derecha de encontrar ( ). Este adjunto se puede escribir de la siguiente manera o de forma más completa: ${\ Displaystyle \ Rightarrow}$${\ Displaystyle \ multimap}$${\ Displaystyle \ to}$${\ Displaystyle Y \ Rightarrow Z}$${\ Displaystyle Z ^ {Y}}$${\ Displaystyle \ Rightarrow: H \ times H \ to H}$${\ Displaystyle \ wedge: H \ times H \ to H}$${\ Displaystyle (- \ wedge Y) \ dashv (Y \ Rightarrow -)}$

Definiciones de la teoría de celosía

Se puede dar una definición equivalente de las álgebras de Heyting considerando las asignaciones:

${\ Displaystyle {\ begin {cases} f_ {a} \ colon H \ to H \\ f_ {a} (x) = a \ wedge x \ end {cases}}}$

para algunos fija una en H . Un retículo acotado H es un álgebra de Heyting si y solo si cada mapeo f _a es el adjunto inferior de una conexión de Galois monótona . En este caso, el adjunto superior respectivo g _a viene dado por g _a ( x ) = a → x , donde → se define como antes.

Sin embargo, otra definición es como una celosía residual cuya operación monoide es ∧. La unidad de monoide debe ser entonces el elemento superior 1. La conmutatividad de este monoide implica que los dos residuos coinciden como a → b .

Celosía acotada con una operación de implicación

Dada una red acotada A con elementos más grandes y más pequeños 1 y 0, y una operación binaria →, estos juntos forman un álgebra de Heyting si y solo si se cumple lo siguiente:

1. ${\ Displaystyle a \ to a = 1}$
2. ${\ Displaystyle a \ wedge (a \ to b) = a \ wedge b}$
3. ${\ Displaystyle b \ wedge (a \ to b) = b}$
4. ${\ Displaystyle a \ to (b \ wedge c) = (a \ to b) \ wedge (a \ to c)}$

donde 4 es la ley distributiva para →.

Caracterización utilizando los axiomas de la lógica intuicionista

Esta caracterización de las álgebras de Heyting hace que la prueba de los hechos básicos relacionados con la relación entre el cálculo proposicional intuicionista y las álgebras de Heyting sea inmediata. (Para estos hechos, consulte las secciones " Identidades probables " y " Construcciones universales ".) Uno debería pensar en el elemento como significando, intuitivamente, "probablemente verdadero". Compare con los axiomas en Lógica intuicionista # Axiomatización ). ${\ Displaystyle \ top}$

Dado un conjunto A con tres operaciones binarias →, ∧ y ∨, y dos elementos distinguidos y , entonces A es un álgebra de Heyting para estas operaciones (y la relación ≤ definida por la condición de que cuando a → b = ) si y solo si el Las siguientes condiciones son válidas para cualquier elemento x , y y z de A : ${\ Displaystyle \ bot}$${\ Displaystyle \ top}$${\ Displaystyle a \ leq b}$${\ Displaystyle \ top}$

1. ${\ displaystyle {\ mbox {If}} x \ leq y {\ mbox {y}} y \ leq x {\ mbox {entonces}} x = y,}$
2. ${\ displaystyle {\ mbox {If}} \ top \ leq y, {\ mbox {entonces}} y = \ top,}$
3. ${\ Displaystyle x \ leq y \ a x,}$
4. ${\ Displaystyle x \ a (y \ a z) \ leq (x \ a y) \ a (x \ a z),}$
5. ${\ Displaystyle x \ land y \ leq x,}$
6. ${\ Displaystyle x \ land y \ leq y,}$
7. ${\ Displaystyle x \ leq y \ to (x \ land y),}$
8. ${\ Displaystyle x \ leq x \ lor y,}$
9. ${\ Displaystyle y \ leq x \ lor y,}$
10. ${\ Displaystyle x \ a z \ leq (y \ a z) \ a (x \ lor y \ a z),}$
11. ${\ Displaystyle \ bot \ leq x.}$

Finalmente, definimos ¬ x como x → . ${\ Displaystyle \ bot}$

La condición 1 dice que deben identificarse fórmulas equivalentes. La condición 2 dice que las fórmulas comprobablemente verdaderas se cierran bajo modus ponens . Las condiciones 3 y 4 son entonces condiciones. Las condiciones 5, 6 y 7 son y condiciones. Las condiciones 8, 9 y 10 son o condiciones. La condición 11 es una condición falsa .

Por supuesto, si se eligiera un conjunto diferente de axiomas para la lógica, podríamos modificar el nuestro en consecuencia.

Ejemplos de

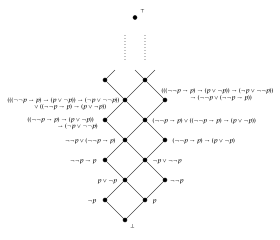
• Todo álgebra de Boole es un álgebra de Heyting, con p → q dado por ¬ p ∨ q .
• Cada conjunto totalmente ordenado que tiene un elemento mínimo 0 y un elemento mayor 1 es un álgebra de Heyting (si se ve como una red). En este caso p → q es igual a 1 cuando p≤q , y q en caso contrario.
• El álgebra de Heyting más simple que aún no es un álgebra booleana es el conjunto totalmente ordenado {0, 1/2, 1} (visto como una celosía), produciendo las operaciones:

  ${\ Displaystyle a \ land b}$ B a 0 1/2 1 0 0 0 0 1/2 0 1/2 1/2 1 0 1/2 1

  ${\ Displaystyle a \ lor b}$ B a 0 1/2 1 0 0 1/2 1 1/2 1/2 1/2 1 1 1 1 1

  a → b B a 0 1/2 1 0 1 1 1 1/2 0 1 1 1 0 1/2 1

  a ¬ a 0 1 1/2 0 1 0

  En este ejemplo, eso 1/2∨¬1/2 = 1/2∨ (1/2 → 0) = 1/2∨0 = 1/2 Falsifica la ley del medio excluido.

• Cada topología proporciona un álgebra de Heyting completa en forma de celosía de conjunto abierto . En este caso, el elemento de A → B es el interior de la unión de un ^C y B , donde A ^c denota el complemento del conjunto abierto A . No todas las álgebras de Heyting completas son de esta forma. Estos problemas se estudian en topología sin sentido , donde las álgebras de Heyting completas también se denominan marcos o localizaciones .
• Cada álgebra interior proporciona un álgebra de Heyting en la forma de su celosía de elementos abiertos. Cada álgebra de Heyting tiene esta forma, ya que un álgebra de Heyting se puede completar a un álgebra booleana tomando su extensión booleana libre como una red distributiva acotada y luego tratándola como una topología generalizada en esta álgebra booleana.
• El álgebra de Lindenbaum de la lógica intuicionista proposicional es un álgebra de Heyting.
• Los elementos globales del clasificador de subobjetos Ω de un topos elemental forman un álgebra de Heyting; es el álgebra de Heyting de valores de verdad de la lógica intuicionista de orden superior inducida por el topos.
• Las álgebras de Łukasiewicz-Moisil (LM _n ) también son álgebras de Heyting para cualquier n (pero no son álgebras MV para n ≥ 5).

Propiedades

Propiedades generales

El orden en un álgebra de Heyting H se puede recuperar de la operación → de la siguiente manera: para cualquier elemento a , b de H , si y solo si a → b = 1. ${\ Displaystyle \ leq}$${\ Displaystyle a \ leq b}$

En contraste con algunas lógicas de muchos valores , las álgebras de Heyting comparten la siguiente propiedad con las álgebras de Boole: si la negación tiene un punto fijo (es decir, ¬ a = a para alguna a ), entonces el álgebra de Heyting es el álgebra de Heyting trivial de un elemento.

Identidades demostrables

Dada una fórmula de cálculo proposicional (utilizando, además de las variables, las conectivas y las constantes 0 y 1), es un hecho, demostrado desde el principio en cualquier estudio de álgebras de Heyting, que las dos condiciones siguientes son equivalentes: ${\ Displaystyle F (A_ {1}, A_ {2}, \ ldots, A_ {n})}$${\ Displaystyle \ land, \ lor, \ lnot, \ to}$

1. La fórmula F es probadamente cierta en el cálculo proposicional intuicionista.
2. La identidad es verdadera para cualquier álgebra H de Heyting y cualquier elemento .${\ Displaystyle F (a_ {1}, a_ {2}, \ ldots, a_ {n}) = 1}$${\ Displaystyle a_ {1}, a_ {2}, \ ldots, a_ {n} \ in H}$

La metaimplicación 1 ⇒ 2 es extremadamente útil y es el principal método práctico para probar identidades en álgebras de Heyting. En la práctica, se usa con frecuencia el teorema de la deducción en tales demostraciones.

Dado que para cualquier a y b en un álgebra de Heyting H tenemos si y solo si a → b = 1, se sigue de 1 ⇒ 2 que siempre que una fórmula F → G sea ​​probadamente cierta, tenemos para cualquier álgebra de Heyting H , y cualquier elementos . (Se deduce del teorema de la deducción que F → G es demostrable [de la nada] si y solo si G es demostrable a partir de F , es decir, si G es una consecuencia demostrable de F ). En particular, si F y G son demostrablemente equivalentes , entonces , dado que ≤ es una relación de orden. ${\ Displaystyle a \ leq b}$${\ Displaystyle F (a_ {1}, a_ {2}, \ ldots, a_ {n}) \ leq G (a_ {1}, a_ {2}, \ ldots, a_ {n})}$${\ Displaystyle a_ {1}, a_ {2}, \ ldots, a_ {n} \ in H}$${\ Displaystyle F (a_ {1}, a_ {2}, \ ldots, a_ {n}) = G (a_ {1}, a_ {2}, \ ldots, a_ {n})}$

1 ⇒ 2 se puede demostrar examinando los axiomas lógicos del sistema de prueba y verificando que su valor es 1 en cualquier álgebra de Heyting, y luego verificando que la aplicación de las reglas de inferencia a expresiones con valor 1 en un álgebra de Heyting da como resultado expresiones con valor 1. Por ejemplo, escojamos el sistema de prueba que tiene modus ponens como su única regla de inferencia, y cuyos axiomas son los del estilo de Hilbert dados en Lógica intuicionista # Axiomatización . Luego, los hechos a verificar se derivan inmediatamente de la definición de álgebras de Heyting, similar a un axioma, dada anteriormente.

1 ⇒ 2 también proporciona un método para probar que ciertas fórmulas proposicionales, aunque son tautologías en la lógica clásica, no pueden probarse en la lógica proposicional intuicionista. Para probar que alguna fórmula no es demostrable, es suficiente exhibir un álgebra H de Heyting y elementos tales que . ${\ Displaystyle F (A_ {1}, A_ {2}, \ ldots, A_ {n})}$${\ Displaystyle a_ {1}, a_ {2}, \ ldots, a_ {n} \ in H}$${\ Displaystyle F (a_ {1}, a_ {2}, \ ldots, a_ {n}) \ neq 1}$

Si se quiere evitar la mención de la lógica, a continuación, en la práctica se hace necesario demostrar que es un lema de una versión del teorema de deducción válida para las álgebra de Heyting: para cualquier elemento de una , b y c de un álgebra de Heyting H , tenemos . ${\ Displaystyle (a \ land b) \ to c = a \ to (b \ to c)}$

Para obtener más información sobre la metaimplicación 2 ⇒ 1, consulte la sección " Construcciones universales " a continuación.

Distributividad

Las álgebras de Heyting son siempre distributivas . En concreto, siempre tenemos las identidades

1. ${\ Displaystyle a \ wedge (b \ vee c) = (a \ wedge b) \ vee (a \ wedge c)}$
2. ${\ Displaystyle a \ vee (b \ wedge c) = (a \ vee b) \ wedge (a \ vee c)}$

La ley distributiva a veces se enuncia como un axioma, pero de hecho se sigue de la existencia de pseudo-complementos relativos. La razón es que, al ser el adjunto inferior de una conexión de Galois , conserva todo suprema existente . La distributividad, a su vez, es solo la preservación del supremo binario por . ${\ Displaystyle \ wedge}$ ${\ Displaystyle \ wedge}$

Mediante un argumento similar, la siguiente ley distributiva infinita se cumple en cualquier álgebra de Heyting completa:

${\ Displaystyle x \ wedge \ bigvee Y = \ bigvee \ {x \ wedge y \ mid y \ in Y \}}$

para cualquier elemento x en H y cualquier subconjunto Y de H . Por el contrario, cualquier retícula completa que satisfaga la ley distributiva infinita anterior es un álgebra de Heyting completa, con

${\ Displaystyle a \ to b = \ bigvee \ {c \ mid a \ land c \ leq b \}}$

siendo su operación relativa de pseudo-complemento.

Elementos regulares y complementados

Un elemento x de un álgebra de Heyting H se llama regular si se cumple alguna de las siguientes condiciones equivalentes:

1. x = ¬¬ x .
2. x = ¬ y para algunos y en H .

La equivalencia de estas condiciones puede ser reexpresada simplemente como la identidad ¬¬¬ x = ¬ x , válido para todo x en H .

Elementos x y y de un Heyting algebra H se denominan complementos una a otra si x ∧ y = 0 y x ∨ y = 1. Si existe, tal y es único y debe de hecho ser igual a ¬ x . Llamamos complementado a un elemento x si admite un complemento. Es cierto que si x se complementa, entonces también lo es ¬ x , y entonces x y ¬ x se complementan entre sí. Sin embargo, de manera confusa, incluso si x no se complementa, ¬ x puede tener un complemento (no igual ax ). En cualquier álgebra de Heyting, los elementos 0 y 1 se complementan entre sí. Por ejemplo, es posible que ¬ x sea ​​0 para cada x diferente de 0, y 1 si x = 0, en cuyo caso 0 y 1 son los únicos elementos regulares.

Cualquier elemento complementado de un álgebra de Heyting es regular, aunque lo contrario no es cierto en general. En particular, 0 y 1 son siempre regulares.

Para cualquier álgebra H de Heyting , las siguientes condiciones son equivalentes:

1. H es un álgebra de Boole ;
2. cada x en H es regular;
3. cada x en H se complementa.

En este caso, el elemento a → b es igual a ¬ a ∨ b .

Los elementos regulares (o complementados) de cualquier álgebra de Heyting H constituyen un álgebra booleana H _reg (resp. H _comp ), en la que las operaciones ∧, ¬ y →, así como las constantes 0 y 1, coinciden con las de H . En el caso de H _borrador , la operación ∨ es también el mismo, por lo tanto, H _borrador es una subálgebra de H . Sin embargo, en general, H _reg no será una subálgebra de H , porque su operación de unión ∨ _reg puede ser diferente de ∨. Para x , y ∈ H _reg , tenemos x ∨ _reg y = ¬ (¬ x ∧ ¬ y ). Consulte a continuación las condiciones necesarias y suficientes para que ∨ _reg coincida con ∨.

Las leyes de De Morgan en un álgebra de Heyting

Una de las dos leyes de De Morgan se satisface en cada álgebra de Heyting, a saber

${\ Displaystyle \ forall x, y \ in H: \ qquad \ lnot (x \ vee y) = \ lnot x \ wedge \ lnot y.}$

Sin embargo, la otra ley de De Morgan no siempre se cumple. En cambio, tenemos una ley de Morgan débil:

${\ Displaystyle \ forall x, y \ in H: \ qquad \ lnot (x \ wedge y) = \ lnot \ lnot (\ lnot x \ vee \ lnot y).}$

Las siguientes afirmaciones son equivalentes para todas las álgebras H de Heyting :

1. H satisface ambas leyes de De Morgan,
2. ${\ Displaystyle \ lnot (x \ wedge y) = \ lnot x \ vee \ lnot y {\ mbox {para todos}} x, y \ en H,}$
3. ${\ Displaystyle \ lnot (x \ wedge y) = \ lnot x \ vee \ lnot y {\ mbox {para todos los regulares}} x, y \ in H,}$
4. ${\ Displaystyle \ lnot \ lnot (x \ vee y) = \ lnot \ lnot x \ vee \ lnot \ lnot y {\ mbox {para todos}} x, y \ en H,}$
5. ${\ Displaystyle \ lnot \ lnot (x \ vee y) = x \ vee y {\ mbox {para todos los regulares}} x, y \ en H,}$
6. ${\ Displaystyle \ lnot (\ lnot x \ wedge \ lnot y) = x \ vee y {\ mbox {para todos los regulares}} x, y \ in H,}$
7. ${\ Displaystyle \ lnot x \ vee \ lnot \ lnot x = 1 {\ mbox {para todos}} x \ en H.}$

La condición 2 es la otra ley de De Morgan. Condición 6 dice que la operación de unión ∨ _reg en el álgebra de Boole H _reg de elementos regulares de H coincide con la operación de ∨ H . La condición 7 establece que todos los elementos regulares están complementados, es decir, H _reg = H _comp .

Demostramos la equivalencia. Claramente, las metaimplicaciones 1 ⇒ 2, 2 ⇒ 3 y 4 ⇒ 5 son triviales. Además, 3 ⇔ 4 y 5 ⇔ 6 resultan simplemente de la primera ley de De Morgan y la definición de elementos regulares. Demostramos que 6 ⇒ 7 tomando ¬ x y ¬¬ x en lugar de x e y en 6 y usando la identidad a ∧ ¬ a = 0. Observe que 2 ⇒ 1 se sigue de la primera ley de De Morgan, y 7 ⇒ 6 resulta del hecho de que la operación de unión ∨ en la subálgebra H _comp es solo la restricción de ∨ a H _comp , teniendo en cuenta las caracterizaciones que hemos dado de las condiciones 6 y 7. La metaimplicación 5 ⇒ 2 es una consecuencia trivial de la la ley de Morgan, teniendo ¬ x y ¬ y en lugar de x e y en 5.

Las álgebras de Heyting que satisfacen las propiedades anteriores están relacionadas con la lógica de De Morgan de la misma manera que las álgebras de Heyting en general están relacionadas con la lógica intuicionista.

Heyting morfismos de álgebra

Definición

Dados dos Heyting álgebras H ₁ y H ₂ y un mapeo f  : H ₁ → H ₂ , se dice que ƒ es un morfismo de álgebras de Heyting si, por cualquier elemento de x y y en H ₁ , tenemos:

1. ${\ Displaystyle f (0) = 0,}$
2. ${\ Displaystyle f (x \ land y) = f (x) \ land f (y),}$
3. ${\ Displaystyle f (x \ lor y) = f (x) \ lor f (y),}$
4. ${\ Displaystyle f (x \ to y) = f (x) \ to f (y),}$

De cualquiera de las últimas tres condiciones (2, 3 o 4) se deduce que f es una función creciente, es decir, que f ( x ) ≤ f ( y ) siempre que x ≤ y .

Suponga que H ₁ y H ₂ son estructuras con operaciones →, ∧, ∨ (y posiblemente ¬) y constantes 0 y 1, y f es un mapeo sobreyectivo de H ₁ a H ₂ con propiedades 1 a 4 anteriores. Entonces, si H ₁ es un álgebra de Heyting, también lo es H ₂ . Esto se deriva de la caracterización de las álgebras de Heyting como retículas acotadas (consideradas como estructuras algebraicas en lugar de conjuntos parcialmente ordenados) con una operación → que satisface ciertas identidades.

Propiedades

El mapa de identidad f ( x ) = x desde cualquier álgebra de Heyting a sí mismo es un morfismo, y el material compuesto g ∘ f de cualesquiera dos morfismos f y g es un morfismo. Por tanto, las álgebras de Heyting forman una categoría .

Ejemplos de

Dada un álgebra de Heyting H y cualquier subálgebra H ₁ , el mapeo de inclusión i  : H ₁ → H es un morfismo.

Para cualquier álgebra de Heyting H , el mapa x ↦ ¬¬ x define un morfismo de H al álgebra de Boole de sus elementos regulares H _reg . Esto es no en un morfismo en general de H a sí mismo, ya que la operación de combinación de H _reg puede ser diferente de la de H .

Cocientes

Deje H un álgebra de Heyting, y dejar F ⊆ H . Llamamos a F un filtro en H si satisface las siguientes propiedades:

1. ${\ Displaystyle 1 \ in F,}$
2. ${\ displaystyle {\ mbox {If}} x, y \ in F {\ mbox {entonces}} x \ land y \ in F,}$
3. ${\ displaystyle {\ mbox {If}} x \ in F, \ y \ in H, \ {\ mbox {y}} x \ leq y {\ mbox {luego}} y \ in F.}$

La intersección de cualquier conjunto de filtros en H es nuevamente un filtro. Por lo tanto, dado cualquier subconjunto S de H hay un filtro más pequeño que contiene S . Lo llamamos el filtro generado por S . Si S está vacío, F = {1}. De lo contrario, F es igual al conjunto de x en H tal que existen y ₁ , y ₂ , ..., y _n ∈ S con y ₁ ∧ y ₂ ∧ ... ∧ y _n ≤ x .

Si H es un álgebra de Heyting y F es un filtro en H , definimos una relación ~ en H de la siguiente manera: escribimos x ~ y cuando x → Y y Y → X tanto pertenecen a F . Entonces ∼ es una relación de equivalencia ; escribimos H / F para el conjunto de cocientes . Existe una estructura de álgebra de Heyting única en H / F tal que la sobreyección canónica p _F  : H → H / F se convierte en un morfismo de álgebra de Heyting. Llamamos a la Heyting algebra H / F del cociente de H por F .

Deje S ser un subconjunto de una Heyting algebra H y dejar que F sea el filtro generado por S . Entonces H / F satisface la siguiente propiedad universal:

Dado cualquier morfismo de Heyting álgebra f  : H → H ' que satisface f ( y ) = 1 para cada y ∈ S , f factores de forma única a través de la surjection canónica p _F  : H → H / F . Es decir, hay un morfismo único f ′  : H / F → H ′ que satisface f′p _F = f . Se dice que el morfismo f ′ es inducido por f .

Sea f  : H ₁ → H ₂ un morfismo de las álgebras de Heyting. El núcleo de f , escrito ker f , es el conjunto f ⁻¹ [{1}]. Es un filtro en H ₁ . (Se debe tener cuidado porque esta definición, si se aplica a un morfismo de álgebras de Boole, es dual con lo que se llamaría el núcleo del morfismo visto como un morfismo de anillos). Por lo anterior, f induce un morfismo f ′  : H ₁ / (ker f ) → H ₂ . Es un isomorfismo de H ₁ / (ker f ) sobre la subálgebra f [ H ₁ ] de H ₂ .

Construcciones universales

Heyting álgebra de fórmulas proposicionales en n variables hasta equivalencia intuicionista

La metaimplicación 2 ⇒ 1 en la sección " Identidades probables " se demuestra mostrando que el resultado de la siguiente construcción es en sí mismo un álgebra de Heyting:

1. Considere el conjunto L de fórmulas proposicionales en las variables A ₁ , A ₂ , ..., A _n .
2. Dotar L con un orden previo ≼ definiendo F ≼ G si G es un (intuitionist) consecuencia lógica de F , es decir, si G es demostrable de F . Es inmediato que ≼ es un pedido anticipado.
3. Considere la relación de equivalencia F ∼ G inducida por el preorden F≼G. (Está definido por F ∼ G si y solo si F ≼ G y G ≼ F. De hecho, ∼ es la relación de equivalencia lógica (intuicionista).)
4. Sea H ₀ el cociente establecido L / ∼. Esta será la álgebra de Heyting deseada.
5. Escribimos [ F ] para la clase de equivalencia de una fórmula F . Operaciones →, ∧, ∨ y ¬ se definen de una manera obvia en L . Verifique que dadas las fórmulas F y G , las clases de equivalencia [ F → G ], [ F ∧ G ], [ F ∨ G ] y [¬ F ] dependen solo de [ F ] y [ G ]. Esto define las operaciones →, ∧, ∨ y ¬ en el cociente conjunto H ₀ = L / ∼. Defina además 1 como la clase de enunciados demostrablemente verdaderos, y establezca 0 = [⊥].
6. Verifique que H ₀ , junto con estas operaciones, sea un álgebra de Heyting. Hacemos esto usando la definición de axioma de álgebras de Heyting. H ₀ satisface las condiciones ENTONCES-1 hasta FALSO porque todas las fórmulas de las formas dadas son axiomas de la lógica intuicionista. MODUS-PONENS se deriva del hecho de que si una fórmula ⊤ → F es demostrablemente verdadera, donde ⊤ es demostrablemente verdadera, entonces F es demostrablemente verdadera (mediante la aplicación de la regla de inferencia modus ponens). Finalmente, EQUIV resulta del hecho de que si F → G y G → F son ambos demostrablemente verdaderos, entonces F y G son probables entre sí (mediante la aplicación de la regla de inferencia modus ponens), por lo tanto [ F ] = [ G ] .

Como siempre bajo la definición de axioma de álgebras de Heyting, definimos ≤ en H ₀ por la condición de que x ≤ y si y solo si x → y = 1. Dado que, según el teorema de la deducción , una fórmula F → G es demostrablemente verdadera si y solo si G se puede demostrar a partir de F , se deduce que [ F ] ≤ [ G ] si y solo si F≼G. En otras palabras, ≤ es la relación de orden en L / ~ inducida por la orden previo ≼ en L .

Álgebra de Heyting gratis en un conjunto arbitrario de generadores

De hecho, la construcción anterior se puede realizar para cualquier conjunto de variables { A _i  : i ∈ I } (posiblemente infinitas). Se obtiene así el álgebra de Heyting libre sobre las variables { A _i }, que de nuevo denotaremos por H ₀ . Es libre en el sentido de que, dado cualquier Heyting algebra H dado junto con una familia de sus elementos < un _i : i ∈ I >, hay un único morfismo f : H ₀ → H satisfacer f ([ A _i ]) = una _yo . La unicidad de f no es difícil de ver, y su existencia resulta esencialmente de la metaimplicación 1 ⇒ 2 de la sección " Identidades demostrables " anterior, en la forma de su corolario de que siempre que F y G son fórmulas demostrablemente equivalentes, F (〈a _i >) = G (< un _i >) para cualquier familia de elementos < un _i > en H .

Heyting álgebra de fórmulas equivalentes con respecto a una teoría T

Dado un conjunto de fórmulas T en las variables { A _i }, vistas como axiomas, la misma construcción podría haberse llevado a cabo con respecto a una relación F ≼ G definida en L para significar que G es una consecuencia demostrable de F y el conjunto de axiomas T . Denotemos por H _T el álgebra de Heyting así obtenida. Entonces H _T satisface la misma propiedad universal como H ₀ anterior, pero con respecto a Heyting álgebra de H y familias de elementos < un _i > que satisfacen la propiedad de que J (< un _i >) = 1 para cualquier axioma J (< A _i > ) en T . (Observemos que H _T , tomado con la familia de sus elementos 〈[ A _i ]〉, satisface esta propiedad por sí misma.) La existencia y unicidad del morfismo se demuestra de la misma manera que para H ₀ , excepto que se debe modificar la metaimplicación 1 ⇒ 2 en " Identidades probables " de modo que 1 dice "probablemente verdadero a partir de T " y 2 dice "cualquier elemento a ₁ , a ₂ , ..., a _n en H que satisfaga las fórmulas de T ".

El álgebra de Heyting H _T que acabamos de definir puede verse como un cociente del álgebra de Heyting libre H ₀ sobre el mismo conjunto de variables, aplicando la propiedad universal de H ₀ con respecto a H _T , y la familia de sus elementos 〈[ A _i ]〉.

Cada álgebra Heyting es isomorfo a una de la forma H _T . Para ver esto, que H sea cualquier álgebra de Heyting, y dejar < un _i : i ∈I> ser una familia de elementos de generación de H (por ejemplo, cualquier familia sobreyectiva). Consideremos ahora el conjunto T de las fórmulas J (< A _i >) en las variables < A _i : i ∈I> tal que J (< un _i >) = 1. Entonces obtenemos un morfismo f : H _T → H por la propiedad universal de H _T , que es claramente sobreyectiva. No es difícil demostrar que f es inyectiva.

Comparación con las álgebras de Lindenbaum

Las construcciones que acabamos de dar juegan un papel completamente análogo con respecto a las álgebras de Heyting al de las álgebras de Lindenbaum con respecto a las álgebras de Boole . De hecho, el álgebra de Lindenbaum B _T en las variables { A _i } con respecto a los axiomas T es solo nuestro H _{T ∪ T 1} , donde T ₁ es el conjunto de todas las fórmulas de la forma ¬¬ F → F , ya que los axiomas adicionales de T ₁ son los únicos que deben agregarse para hacer demostrables todas las tautologías clásicas.

Heyting álgebras aplicadas a la lógica intuicionista

Si uno interpreta los axiomas de la lógica proposicional intuicionista como términos de un álgebra de Heyting, entonces evaluarán al elemento más grande, 1, en cualquier álgebra de Heyting bajo cualquier asignación de valores a las variables de la fórmula. Por ejemplo, ( P ∧ Q ) → P es, por definición del pseudo-complemento, el elemento más grande x tal que . Esta inecuación se satisface para cualquier x , por lo que el mayor de tales x es 1. ${\ Displaystyle P \ land Q \ land x \ leq P}$

Además, la regla de modus ponens nos permite derivar la fórmula Q partir de las fórmulas P y P → Q . Pero en cualquier álgebra de Heyting, si P tiene el valor 1 y P → Q tiene el valor 1, entonces significa eso , y así ; solo puede ser que Q tenga el valor 1. ${\ Displaystyle P \ land 1 \ leq Q}$${\ Displaystyle 1 \ land 1 \ leq Q}$

Esto significa que si una fórmula es deducible de las leyes de la lógica intuicionista, derivada de sus axiomas por medio de la regla del modus ponens, entonces siempre tendrá el valor 1 en todas las álgebras de Heyting bajo cualquier asignación de valores a las variables de la fórmula. . Sin embargo, se puede construir un álgebra de Heyting en la que el valor de la ley de Peirce no siempre sea 1. Considere el álgebra de 3 elementos {0,1/2, 1} como se indica arriba. Si asignamos1/2a P y 0 a Q , entonces el valor de la ley de Peirce (( P → Q ) → P ) → P es1/2. De ello se deduce que la ley de Peirce no puede derivarse intuicionistamente. Ver isomorfismo de Curry-Howard para el contexto general de lo que esto implica en la teoría de tipos .

También se puede probar lo contrario: si una fórmula siempre tiene el valor 1, entonces es deducible de las leyes de la lógica intuicionista, por lo que las fórmulas intuicionistas válidas son exactamente aquellas que siempre tienen un valor de 1. Esto es similar a la noción que las fórmulas clásicamente válidas son aquellas fórmulas que tienen un valor de 1 en el álgebra booleana de dos elementos bajo cualquier posible asignación de verdadero y falso a las variables de la fórmula, es decir, son fórmulas que son tautologías en el sentido habitual de tabla de verdad. Un álgebra de Heyting, desde el punto de vista lógico, es entonces una generalización del sistema habitual de valores de verdad, y su elemento más grande 1 es análogo a "verdadero". El sistema lógico de dos valores habitual es un caso especial de un álgebra de Heyting, y el más pequeño no trivial, en el que los únicos elementos del álgebra son 1 (verdadero) y 0 (falso).

Problemas de decisión

El problema de si una ecuación dada se cumple en cada álgebra de Heyting fue decidible por S. Kripke en 1965. La complejidad computacional precisa del problema fue establecida por R. Statman en 1979, quien demostró que era PSPACE-completo y, por lo tanto, en menos tan difícil como decidir ecuaciones de álgebra de Boole (mostrado coNP-completo en 1971 por S. Cook) y conjeturado que es considerablemente más difícil. La teoría elemental o de primer orden de las álgebras de Heyting es indecidible. Queda abierto si la teoría universal de Horn de las álgebras de Heyting, o el problema verbal , es decidible. A propósito del problema verbal, se sabe que las álgebras de Heyting no son localmente finitas (ninguna álgebra de Heyting generada por un conjunto finito no vacío es finita), en contraste con las álgebras booleanas que son localmente finitas y cuyo problema verbal es decidible. Se desconoce si existen álgebras de Heyting completas libres excepto en el caso de un solo generador donde el álgebra de Heyting libre en un generador se puede completar trivialmente al unir un nuevo top.

Representación topológica y teoría de la dualidad

Cada álgebra de Heyting H es naturalmente isomórfica a una subred delimitada L de conjuntos abiertos de un espacio topológico X , donde la implicación de L viene dada por el interior de . Más precisamente, X es el espacio espectral de ideales primos de la acotada celosía H y L es la celosía de subconjuntos abiertos y cuasi-compacto de X . ${\ Displaystyle U \ a V}$${\ Displaystyle (X \ setminus U) \ cup V}$

De manera más general, la categoría de álgebras de Heyting es doblemente equivalente a la categoría de espacios de Heyting. Esta dualidad puede verse como una restricción de la dualidad clásica de Stone de retículas distributivas limitadas a la subcategoría (no completa) de las álgebras de Heyting.

Alternativamente, la categoría de álgebras de Heyting es doblemente equivalente a la categoría de espacios de Esakia . A esto se le llama dualidad de Esakia .

Notas

Ver también

• Topología Alexandrov
• Lógicas superintuicionistas (también conocidas como intermedias)
• Lista de temas de álgebra de Boole
• Álgebra de Ockham

Referencias

• Rutherford, Daniel Edwin (1965). Introducción a la teoría de celosía . Oliver y Boyd. OCLC  224572 .
• F. Borceux, Manual de álgebra categórica 3 , En la Enciclopedia de las matemáticas y sus aplicaciones , Vol. 53, Cambridge University Press, 1994. ISBN  0-521-44180-3 OCLC  52238554
• G. Gierz, KH Hoffmann, K. Keimel, JD Lawson, M. Mislove y DS Scott, Continuous Lattices and Domains , In Encyclopedia of Mathematics and its Applications , Vol. 93, Cambridge University Press, 2003.
• S. Ghilardi. Álgebras de Heyting libres como álgebras bi-Heyting , Matemáticas. Rep. Acad. Sci. Canadá XVI., 6: 240–244, 1992.
• Heyting, A. (1930), "Die formalen Regeln der intuitionistischen Logik. I, II, III", Sitzungsberichte Akad. Berlín : 42–56, 57–71, 158–169, JFM  56.0823.01
• Dickmann, Max; Schwartz, Niels; Tressl, Marcus (2019). Espacios espectrales . Nuevas monografías matemáticas. 35 . Cambridge: Cambridge University Press . doi : 10.1017 / 9781316543870 . ISBN 9781107146723. S2CID  201542298 .

enlaces externos

• Heyting álgebra en PlanetMath .