Fenómeno de Runge - Runge's phenomenon

La función Runge (rojo, pico central más alto); el polinomio de interpolación de quinto orden con puntos de interpolación igualmente espaciados (azul, pico central más bajo); y el polinomio de interpolación de noveno orden con puntos de interpolación igualmente espaciados (verde, pico central medio)

En el campo matemático del análisis numérico , el fenómeno de Runge ( alemán: [ˈʁʊŋə] ) es un problema de oscilación en los bordes de un intervalo que ocurre cuando se usa la interpolación polinómica con polinomios de alto grado sobre un conjunto de puntos de interpolación equiespaciados. Fue descubierto por Carl David Tolmé Runge (1901) al explorar el comportamiento de los errores al usar la interpolación polinomial para aproximar ciertas funciones. El descubrimiento fue importante porque muestra que ir a grados más altos no siempre mejora la precisión. El fenómeno es similar al fenómeno de Gibbs en aproximaciones de series de Fourier.

Introducción

El teorema de aproximación de Weierstrass establece que para cada función continua f ( x ) definida en un intervalo [ a , b ], existe un conjunto de funciones polinomiales P _n ( x ) para n = 0, 1, 2,…, cada una de grado a lo sumo n , que se aproxima a f ( x ) con convergencia uniforme sobre [ a , b ] cuando n tiende a infinito, es decir,

${\ Displaystyle \ lim _ {n \ rightarrow \ infty} \ left (\ max _ {a \ leq x \ leq b} \ left | f (x) -P_ {n} (x) \ right | \ right) = 0.}$

Considere el caso en el que se desea interpolar a través de n +1 puntos equiespaciados de una función f ( x ) utilizando el polinomio de n grados P _n ( x ) que pasa por esos puntos. Naturalmente, uno podría esperar del teorema de Weierstrass que el uso de más puntos conduciría a una reconstrucción más precisa de f ( x ). Sin embargo, no se garantiza que este conjunto particular de funciones polinomiales P _n ( x ) tenga la propiedad de convergencia uniforme; el teorema solo establece que existe un conjunto de funciones polinomiales, sin proporcionar un método general para encontrar una .

El P _n ( x ) producido de esta manera puede de hecho divergir de f ( x ) a medida que n aumenta; esto ocurre típicamente en un patrón oscilante que aumenta cerca de los extremos de los puntos de interpolación. Este fenómeno se atribuye a Runge.

Problema

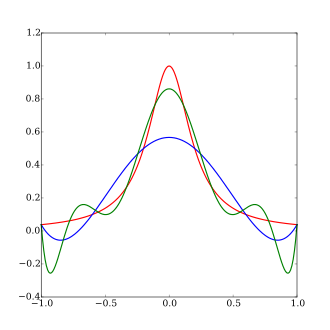
Considere la función Runge

${\ Displaystyle f (x) = {\ frac {1} {1 + 25x ^ {2}}} \,}$

(una versión a escala de la Bruja de Agnesi ). Runge descubrió que si esta función se interpola en puntos equidistantes x _i entre -1 y 1 de manera que:

${\ Displaystyle x_ {i} = {\ frac {2i} {n}} - 1, \ quad i \ in \ left \ {0,1, \ dots, n \ right \}}$

con un polinomio P _n ( x ) de grado ≤  n , la interpolación resultante oscila hacia el final del intervalo, es decir, cerca de -1 y 1. Incluso se puede demostrar que el error de interpolación aumenta (sin límite) cuando el grado de el polinomio aumenta:

${\ Displaystyle \ lim _ {n \ rightarrow \ infty} \ left (\ max _ {- 1 \ leq x \ leq 1} | f (x) -P_ {n} (x) | \ right) = \ infty. }$

Esto muestra que la interpolación polinomial de alto grado en puntos equidistantes puede ser problemática.

Razón

El fenómeno de Runge es consecuencia de dos propiedades de este problema.

• La magnitud de las derivadas de n -ésimo orden de esta función particular crece rápidamente cuando n aumenta.
• La equidistancia entre puntos conduce a una constante de Lebesgue que aumenta rápidamente cuando n aumenta.

El fenómeno es gráficamente obvio porque ambas propiedades se combinan para aumentar la magnitud de las oscilaciones.

El error entre la función generadora y el polinomio de interpolación de orden n viene dado por

${\ Displaystyle f (x) -P_ {n} (x) = {\ frac {f ^ {(n + 1)} (\ xi)} {(n + 1)!}} \ prod _ {i = 0 } ^ {n} (x-x_ {i})}$

para algunos en (-1, 1). Por lo tanto, ${\ Displaystyle \ xi}$

${\ Displaystyle \ max _ {- 1 \ leq x \ leq 1} | f (x) -P_ {n} (x) | \ leq \ max _ {- 1 \ leq x \ leq 1} {\ frac {\ izquierda | f ^ {(n + 1)} (x) \ derecha |} {(n + 1)!}} \ max _ {- 1 \ leq x \ leq 1} \ prod _ {i = 0} ^ { n} | x-x_ {i} |}$.

Denotar por la función nodal ${\ Displaystyle w_ {n} (x)}$

${\ Displaystyle w_ {n} (x) = (x-x_ {0}) (x-x_ {1}) \ cdots (x-x_ {n})}$

y sea ​​el máximo de la magnitud de la función: ${\ Displaystyle W_ {n}}$${\ Displaystyle w_ {n}}$

${\ Displaystyle W_ {n} = \ max _ {- 1 \ leq x \ leq 1} | w_ {n} (x) |}$.

Es elemental demostrar que con nodos equidistantes

${\ Displaystyle W_ {n} \ leq n! h ^ {n + 1}}$

donde es el tamaño del paso. ${\ Displaystyle h = 2 / n}$

Además, suponga que la ( n +1) -ésima derivada de está acotada, es decir ${\ Displaystyle f}$

${\ Displaystyle \ max _ {- 1 \ leq x \ leq 1} | f ^ {(n + 1)} (x) | \ leq M_ {n + 1}}$.

Por lo tanto,

${\ Displaystyle \ max _ {- 1 \ leq x \ leq 1} | f (x) -P_ {n} (x) | \ leq M_ {n + 1} {\ frac {h ^ {n + 1}} {(n + 1)}}}$.

Pero la magnitud de la derivada ( n +1) -ésima de la función de Runge aumenta cuando n aumenta, ya que . La consecuencia es que el límite superior resultante , tiende al infinito cuando n tiende al infinito. ${\ Displaystyle M_ {n + 1} \ leq (n + 1)! 5 ^ {n + 1}}$${\ Displaystyle (10 / n) ^ {n + 1} n!}$

Aunque se utiliza a menudo para explicar el fenómeno de Runge, el hecho de que el límite superior del error llegue al infinito no implica necesariamente, por supuesto, que el error en sí también diverja con n.

Mitigaciones al problema

Cambio de puntos de interpolación

La oscilación se puede minimizar mediante el uso de nodos que se distribuyen más densamente hacia los bordes del intervalo, específicamente, con densidad asintótica (en el intervalo [−1,1]) dada por la fórmula . Un ejemplo estándar de tal conjunto de nodos son los nodos de Chebyshev , para los cuales se garantiza que el error máximo en la aproximación de la función de Runge disminuirá al aumentar el orden polinomial. El fenómeno demuestra que los polinomios de alto grado generalmente no son adecuados para la interpolación con nodos equidistantes. ${\ Displaystyle 1 / {\ sqrt {1-x ^ {2}}}}$

Algoritmo S-Runge sin remuestreo

Cuando se deben utilizar muestras equidistantes porque el remuestreo en conjuntos de nodos con buen comportamiento no es factible, se puede considerar el algoritmo S-Runge. En este enfoque, el conjunto original de nodos se asigna al conjunto de nodos de Chebyshev , lo que proporciona una reconstrucción polinomial estable. La peculiaridad de este método es que no es necesario volver a muestrear en los nodos mapeados, que también se denominan nodos falsos . Puede encontrar una implementación de Python de este procedimiento aquí .

Uso de polinomios por partes

El problema se puede evitar mediante el uso de curvas spline que son polinomios por partes. Cuando se intenta disminuir el error de interpolación, se puede aumentar el número de piezas polinomiales que se utilizan para construir la spline en lugar de aumentar el grado de polinomios utilizados.

Minimización restringida

También se puede ajustar un polinomio de mayor grado (por ejemplo, con puntos use un polinomio de orden en lugar de ), y ajustar un polinomio de interpolación cuya primera (o segunda) derivada tiene una norma mínima . ${\ Displaystyle n}$${\ Displaystyle N = n ^ {2}}$${\ Displaystyle n + 1}$${\ Displaystyle L ^ {2}}$

Un enfoque similar consiste en minimizar una versión restringida de la distancia entre la derivada del polinomio y el valor medio de su derivada. Explícitamente, para minimizar ${\ Displaystyle L ^ {p}}$${\ Displaystyle m ^ {\ mathrm {th}}}$${\ Displaystyle m ^ {\ mathrm {th}}}$

${\ Displaystyle V_ {p} = \ int _ {a} ^ {b} \ left | {\ frac {\ operatorname {d} ^ {m} P_ {N} (x)} {\ operatorname {d} x ^ {m}}} - {\ frac {1} {ba}} \ int _ {a} ^ {b} {\ frac {\ operatorname {d} ^ {m} P_ {N} (z)} {\ operatorname {d} z ^ {m}}} \ operatorname {d} z \ right | ^ {p} \ operatorname {d} x- \ sum _ {i = 1} ^ {n} \ lambda _ {i} \, \ izquierda (P_ {N} (x_ {i}) - f (x_ {i}) \ derecha),}$

donde y , con respecto a los coeficientes del polinomio y los multiplicadores de Lagrange , . Cuando , las ecuaciones de restricción generadas por los multiplicadores de Lagrange se reducen al polinomio mínimo que pasa por todos los puntos. En el extremo opuesto, se acercará a una forma muy similar a una aproximación de polinomios por partes. Cuando , en particular, se aproxima a los polinomios lineales a trozos, es decir, conectando los puntos de interpolación con líneas rectas. ${\ Displaystyle N \ geq n-1}$${\ Displaystyle m <N}$${\ Displaystyle \ lambda _ {i}}$${\ Displaystyle N = n-1}$${\ Displaystyle P_ {N} (x)}$${\ Displaystyle n}$${\ Displaystyle \ lim _ {N \ rightarrow \ infty} P_ {N} (x)}$${\ Displaystyle m = 1}$${\ Displaystyle \ lim _ {N \ rightarrow \ infty} P_ {N} (x)}$

El papel que juega en el proceso de minimización es controlar la importancia del tamaño de las fluctuaciones alejándose del valor medio. Cuanto más grande es, más grandes fluctuaciones se penalizan en comparación con las pequeñas. La mayor ventaja de la norma euclidiana , es que permite soluciones analíticas y garantiza que solo tendrá un mínimo. Cuando puede haber varios mínimos , es difícil garantizar que un mínimo particular encontrado sea el mínimo global en lugar de uno local. ${\ Displaystyle p}$${\ Displaystyle V_ {p}}$${\ Displaystyle p}$${\ Displaystyle p = 2}$${\ Displaystyle V_ {p}}$${\ Displaystyle p \ neq 2}$${\ Displaystyle V_ {p}}$

Ajuste de mínimos cuadrados

Otro método consiste en ajustar un polinomio de menor grado utilizando el método de mínimos cuadrados . Generalmente, cuando se utilizan puntos equidistantes, la aproximación por mínimos cuadrados está bien condicionada. ${\ Displaystyle m}$${\ Displaystyle N <2 {\ sqrt {m}}}$${\ Displaystyle P_ {N} (x)}$

Polinomio de Bernstein

Usando polinomios de Bernstein , uno puede aproximar uniformemente cada función continua en un intervalo cerrado, aunque este método es bastante caro computacionalmente.

Interpolación de restricciones falsas externas

Este método propone apilar de manera óptima una distribución densa de restricciones del tipo P "(x) = 0 en nodos colocados externamente cerca de los extremos de cada lado del intervalo de interpolación, donde P" (x) es la segunda derivada del polinomio de interpolación . Esas restricciones se denominan Restricciones falsas externas ya que no pertenecen al intervalo de interpolación y no coinciden con el comportamiento de la función Runge. El método ha demostrado que tiene un mejor rendimiento de interpolación que los polinomios por partes (splines) para mitigar el fenómeno de Runge.

Declaraciones relacionadas de la teoría de la aproximación

Para cada tabla predefinida de nodos de interpolación hay una función continua para la cual la secuencia de polinomios de interpolación en esos nodos diverge. Para cada función continua hay una tabla de nodos en los que converge el proceso de interpolación. La interpolación de Chebyshev (es decir, en los nodos de Chebyshev ) converge uniformemente para cada función absolutamente continua.

Ver también

• Compare con el fenómeno de Gibbs para funciones de base sinusoidal
• Serie de taylor
• Nódulos de Chebyshev
• Linterna Schwarz , otro ejemplo de fracaso de la convergencia
• Teorema de Stone-Weierstrass

Referencias