Polinomio de Lagrange - Lagrange polynomial

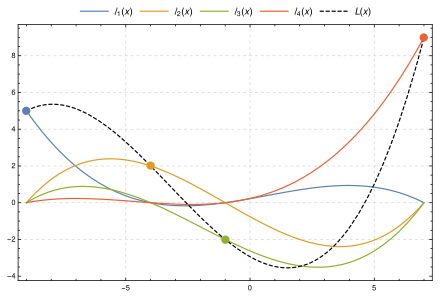
Esta imagen muestra, para cuatro puntos ( (−9, 5) , (−4, 2) , (−1, −2) , (7, 9) ), el polinomio de interpolación (cúbico) L ( x ) (discontinuo, negro), que es la suma de los polinomios base escalados y ₀ ℓ ₀ ( x ) , y ₁ ℓ ₁ ( x ) , y ₂ ℓ ₂ ( x ) y y ₃ ℓ ₃ ( x ) . El polinomio de interpolación pasa por los cuatro puntos de control, y cada polinomio base escalado pasa por su respectivo punto de control y es 0 donde x corresponde a los otros tres puntos de control.

En el análisis numérico , los polinomios de Lagrange se utilizan para la interpolación de polinomios . Para un conjunto dado de puntos sin dos valores iguales, el polinomio de Lagrange es el polinomio de menor grado que asume en cada valor el valor correspondiente , por lo que las funciones coinciden en cada punto. ${\ Displaystyle (x_ {j}, y_ {j})}$${\ Displaystyle x_ {j}}$${\ Displaystyle x_ {j}}$${\ Displaystyle y_ {j}}$

Aunque lleva el nombre de Joseph-Louis Lagrange , quien lo publicó en 1795, el método fue descubierto por primera vez en 1779 por Edward Waring . También es una consecuencia fácil de una fórmula publicada en 1783 por Leonhard Euler .

Los usos de los polinomios de Lagrange incluyen el método Newton-Cotes de integración numérica y el esquema de intercambio secreto de Shamir en criptografía .

La interpolación de Lagrange es susceptible al fenómeno de gran oscilación de Runge . Como cambiar los puntos requiere recalcular todo el interpolante, a menudo es más fácil usar polinomios de Newton . ${\ Displaystyle x_ {j}}$

Definición

Aquí trazamos las funciones de base de Lagrange de primer, segundo y tercer orden en un dominio de dos unidades. Se utilizan combinaciones lineales de funciones de base de Lagrange para construir polinomios de interpolación de Lagrange. Las funciones de base de Lagrange se utilizan comúnmente en el análisis de elementos finitos como bases para las funciones de forma de los elementos. Además, es común utilizar un dominio de dos unidades como espacio natural para la definición del elemento finito.

Dado un conjunto de k  + 1 puntos de datos

${\ Displaystyle (x_ {0}, y_ {0}), \ ldots, (x_ {j}, y_ {j}), \ ldots, (x_ {k}, y_ {k})}$

donde no hay dos iguales, el polinomio de interpolación en la forma de Lagrange es una combinación lineal${\ Displaystyle x_ {j}}$

${\ Displaystyle L (x): = \ sum _ {j = 0} ^ {k} y_ {j} \ ell _ {j} (x)}$

de polinomios de base de Lagrange

${\ Displaystyle \ ell _ {j} (x): = \ prod _ {\ begin {smallmatrix} 0 \ leq m \ leq k \\ m \ neq j \ end {smallmatrix}} {\ frac {x-x_ { m}} {x_ {j} -x_ {m}}} = {\ frac {(x-x_ {0})} {(x_ {j} -x_ {0})}} \ cdots {\ frac {( x-x_ {j-1})} {(x_ {j} -x_ {j-1})}} {\ frac {(x-x_ {j + 1})} {(x_ {j} -x_ { j + 1})}} \ cdots {\ frac {(x-x_ {k})} {(x_ {j} -x_ {k})}},}$

donde . Observe cómo, dada la suposición inicial de que no hay dos iguales, entonces (cuándo ) , por lo que esta expresión siempre está bien definida. La razón por pares con no están permitidos es que ninguna función de interpolación de tal manera que existiría; una función solo puede obtener un valor para cada argumento . Por otro lado, si también , entonces esos dos puntos serían en realidad un solo punto. ${\ Displaystyle 0 \ leq j \ leq k}$${\ Displaystyle x_ {j}}$${\ Displaystyle m \ neq j}$${\ Displaystyle x_ {j} -x_ {m} \ neq 0}$${\ Displaystyle x_ {i} = x_ {j}}$${\ Displaystyle y_ {i} \ neq y_ {j}}$${\ Displaystyle L}$${\ Displaystyle y_ {i} = L (x_ {i})}$${\ Displaystyle x_ {i}}$${\ Displaystyle y_ {i} = y_ {j}}$

Para todos , incluye el término en el numerador, por lo que todo el producto será cero en : ${\ Displaystyle i \ neq j}$${\ Displaystyle \ ell _ {j} (x)}$${\ Displaystyle (x-x_ {i})}$${\ Displaystyle x = x_ {i}}$

${\ Displaystyle \ forall ({j \ neq i}): \ ell _ {j} (x_ {i}) = \ prod _ {m \ neq j} {\ frac {x_ {i} -x_ {m}} {x_ {j} -x_ {m}}} = {\ frac {(x_ {i} -x_ {0})} {(x_ {j} -x_ {0})}} \ cdots {\ frac {( x_ {i} -x_ {i})} {(x_ {j} -x_ {i})}} \ cdots {\ frac {(x_ {i} -x_ {k})} {(x_ {j} - x_ {k})}} = 0.}$

Por otra parte,

$${\ Displaystyle \ ell _ {j} (x_ {j}): = \ prod _ {m \ neq j} {\ frac {x_ {j} -x_ {m}} {x_ {j} -x_ {m} }} = 1}$$

En otras palabras, todos los polinomios de base son cero en , excepto , para el cual mantiene eso , porque carece del término. ${\ Displaystyle x = x_ {j}}$${\ Displaystyle \ ell _ {j} (x)}$${\ Displaystyle \ ell _ {j} (x_ {j}) = 1}$${\ Displaystyle (x-x_ {j})}$

De ello se desprende que , por lo que en cada punto , mostrando que interpola la función exactamente. ${\ Displaystyle y_ {j} \ ell _ {j} (x_ {j}) = y_ {j}}$${\ Displaystyle x_ {j}}$${\ Displaystyle L (x_ {j}) = y_ {j} + 0 + 0 + \ dots + 0 = y_ {j}}$${\ Displaystyle L}$

Prueba

La función L ( x ) que se busca es un polinomio en x del menor grado que interpola el conjunto de datos dado; es decir, asume el valor y _j en el correspondiente x _j para todos los puntos de datos j :

${\ Displaystyle L (x_ {j}) = y_ {j} \ qquad j = 0, \ ldots, k.}$

Observa eso:

• En hay k factores en el producto y cada factor contiene uno x , por lo que L ( x ) (que es una suma de estos k polinomios -Grado) debe ser un polinomio de grado a lo sumo k .${\ Displaystyle \ ell _ {j} (x)}$
• ${\ Displaystyle \ ell _ {j} (x_ {i}) = \ prod _ {\ begin {smallmatrix} m = 0 \\ m \ neq j \ end {smallmatrix}} ^ {k} {\ frac {x_ { i} -x_ {m}} {x_ {j} -x_ {m}}}.}$

Expanda este producto. Dado que el producto omite el término donde m = j , si i = j entonces todos los términos que aparecen son . Además, si i ≠ j, entonces un término en el producto será (para m = i ) ,, poniendo a cero todo el producto. Entonces, ${\ Displaystyle {\ frac {x_ {j} -x_ {m}} {x_ {j} -x_ {m}}} = 1}$${\ Displaystyle {\ frac {x_ {i} -x_ {i}} {x_ {j} -x_ {i}}} = 0}$

${\ Displaystyle \ ell _ {j} (x_ {i}) = \ delta _ {ji} = {\ begin {cases} 1, & {\ text {if}} j = i \\ 0, & {\ text {if}} j \ neq i \ end {cases}},}$

¿Dónde está el delta de Kronecker ? Entonces: ${\ Displaystyle \ delta _ {ij}}$

${\ Displaystyle L (x_ {i}) = \ sum _ {j = 0} ^ {k} y_ {j} \ ell _ {j} (x_ {i}) = \ sum _ {j = 0} ^ { k} y_ {j} \ delta _ {ji} = y_ {i}.}$

Por tanto, la función L ( x ) es un polinomio con grado como máximo k y donde L ( x _i ) = y _i .

Además, el polinomio de interpolación es único, como lo muestra el teorema de unisolvencia en el artículo de interpolación del polinomio .

También es cierto que:

${\ Displaystyle \ sum _ {j = 0} ^ {k} \ ell _ {j} (x) = 1 \ qquad \ forall x}$

ya que debe ser un polinomio de grado, como máximo, ky pasa por todos estos k  + 1 puntos de datos:

${\ Displaystyle (x_ {0}, 1), \ ldots, (x_ {j}, 1), \ ldots, (x_ {k}, 1)}$

resultando en una línea horizontal, ya que una línea recta es el único polinomio de grado menor que k  + 1 que pasa por k  + 1 puntos alineados.

Una perspectiva del álgebra lineal

Resolver un problema de interpolación conduce a un problema de álgebra lineal que equivale a la inversión de una matriz. Usando una base monomial estándar para nuestro polinomio de interpolación , debemos invertir la matriz de Vandermonde para resolver los coeficientes de . Al elegir una mejor base, la base de Lagrange, nos limitamos obtenemos la matriz de identidad , que es su propio inverso: la base de Lagrange automáticamente invierte el análogo de la matriz de Vandermonde. ${\ textstyle L (x) = \ sum _ {j = 0} ^ {k} x ^ {j} m_ {j}}$ ${\ Displaystyle (x_ {i}) ^ {j}}$${\ Displaystyle L (x_ {i}) = y_ {i}}$${\ Displaystyle m_ {j}}$${\ Displaystyle L (x)}$${\ textstyle L (x) = \ sum _ {j = 0} ^ {k} l_ {j} (x) y_ {j}}$${\ Displaystyle \ delta _ {ij}}$

Esta construcción es análoga al teorema chino del resto . En lugar de buscar restos de números enteros modulo primos, buscamos restos de polinomios cuando se dividen por lineales.

Además, cuando el orden es grande, se puede usar la Transformación Rápida de Fourier para resolver los coeficientes del polinomio interpolado.

Ejemplos de

Ejemplo 1

Deseamos interpolar ƒ ( x ) =  x ² en el rango 1 ≤  x  ≤ 3, dados estos tres puntos:

${\ Displaystyle {\ begin {alineado} x_ {0} & = 1 &&& f (x_ {0}) & = 1 \\ x_ {1} & = 2 &&& f (x_ {1}) & = 4 \\ x_ {2} & = 3 &&& f (x_ {2}) & = 9. \ end {alineado}}}$

El polinomio de interpolación es:

${\ Displaystyle {\ begin {alineado} L (x) & = {1} \ cdot {x-2 \ over 1-2} \ cdot {x-3 \ over 1-3} + {4} \ cdot {x -1 \ over 2-1} \ cdot {x-3 \ over 2-3} + {9} \ cdot {x-1 \ over 3-1} \ cdot {x-2 \ over 3-2} \\ [10pt] & = x ^ {2}. \ End {alineado}}}$

Ejemplo 2

Deseamos interpolar ƒ ( x ) =  x ³ en el rango 1 ≤  x  ≤ 4, dados estos cuatro puntos:

${\ Displaystyle x_ {0} = 1}$	${\ Displaystyle f (x_ {0}) = 1}$
${\ Displaystyle x_ {1} = 2}$	${\ Displaystyle f (x_ {1}) = 8}$
${\ Displaystyle x_ {2} = 3}$	${\ Displaystyle f (x_ {2}) = 27}$
${\ Displaystyle x_ {3} = 4}$	${\ Displaystyle f (x_ {3}) = 64}$

El polinomio de interpolación es:

${\ Displaystyle {\ begin {alineado} L (x) & = {1} \ cdot {x-2 \ over 1-2} \ cdot {x-3 \ over 1-3} \ cdot {x-4 \ over 1-4} + {8} \ cdot {x-1 \ over 2-1} \ cdot {x-3 \ over 2-3} \ cdot {x-4 \ over 2-4} + {27} \ cdot {x-1 \ over 3-1} \ cdot {x-2 \ over 3-2} \ cdot {x-4 \ over 3-4} + {64} \ cdot {x-1 \ over 4-1} \ cdot {x-2 \ over 4-2} \ cdot {x-3 \ over 4-3} \\ [8pt] & = x ^ {3} \ end {alineado}}}$

Notas

Ejemplo de divergencia de interpolación para un conjunto de polinomios de Lagrange.

La forma de Lagrange del polinomio de interpolación muestra el carácter lineal de la interpolación polinomial y la unicidad del polinomio de interpolación. Por tanto, se prefiere en pruebas y argumentos teóricos. La singularidad también se puede ver en la invertibilidad de la matriz de Vandermonde, debido a la no desaparición del determinante de Vandermonde .

Pero, como se puede ver en la construcción, cada vez que un nodo x _k cambia, todos los polinomios de base de Lagrange deben recalcularse. Una forma mejor del polinomio de interpolación para propósitos prácticos (o computacionales) es la forma baricéntrica de la interpolación de Lagrange (ver más abajo) o polinomios de Newton .

Lagrange y otras interpolaciones en puntos igualmente espaciados, como en el ejemplo anterior, producen un polinomio que oscila por encima y por debajo de la función verdadera. Este comportamiento tiende a crecer con el número de puntos, dando lugar a una divergencia conocida como fenómeno de Runge ; el problema puede eliminarse eligiendo puntos de interpolación en los nodos de Chebyshev .

Los polinomios de base de Lagrange se pueden utilizar en la integración numérica para derivar las fórmulas de Newton-Cotes .

Forma baricéntrica

Utilizando

${\ Displaystyle \ ell (x) = (x-x_ {0}) (x-x_ {1}) \ cdots (x-x_ {k})}$

${\ Displaystyle \ ell '(x_ {j}) = {\ frac {\ mathrm {d} \ ell (x)} {\ mathrm {d} x}} {\ Big |} _ {x = x_ {j} } = \ prod _ {i = 0, i \ neq j} ^ {k} (x_ {j} -x_ {i})}$

podemos reescribir los polinomios de base de Lagrange como

${\ Displaystyle \ ell _ {j} (x) = {\ frac {\ ell (x)} {\ ell '(x_ {j}) (x-x_ {j})}}}$

o, definiendo los pesos baricéntricos

${\ Displaystyle w_ {j} = {\ frac {1} {\ ell '(x_ {j})}}}$

simplemente podemos escribir

${\ Displaystyle \ ell _ {j} (x) = \ ell (x) {\ frac {w_ {j}} {x-x_ {j}}}}$

que se conoce comúnmente como la primera forma de la fórmula de interpolación baricéntrica.

La ventaja de esta representación es que el polinomio de interpolación ahora se puede evaluar como

${\ Displaystyle L (x) = \ ell (x) \ sum _ {j = 0} ^ {k} {\ frac {w_ {j}} {x-x_ {j}}} y_ {j}}$

que, si los pesos se han calculado previamente, requiere solo operaciones (evaluación y los pesos ) en lugar de evaluar los polinomios de base de Lagrange individualmente. ${\ Displaystyle w_ {j}}$${\ Displaystyle {\ mathcal {O}} (k)}$${\ Displaystyle \ ell (x)}$${\ Displaystyle w_ {j} / (x-x_ {j})}$${\ Displaystyle {\ mathcal {O}} (k ^ {2})}$${\ Displaystyle \ ell _ {j} (x)}$

La fórmula de interpolación baricéntrica también se puede actualizar fácilmente para incorporar un nuevo nodo dividiendo cada uno de los , por y construyendo el nuevo como se indicó anteriormente. ${\ Displaystyle x_ {k + 1}}$${\ Displaystyle w_ {j}}$${\ Displaystyle j = 0 \ dots k}$${\ Displaystyle (x_ {j} -x_ {k + 1})}$${\ Displaystyle w_ {k + 1}}$

Podemos simplificar aún más la primera forma considerando primero la interpolación baricéntrica de la función constante : ${\ Displaystyle g (x) \ equiv 1}$

${\ Displaystyle g (x) = \ ell (x) \ sum _ {j = 0} ^ {k} {\ frac {w_ {j}} {x-x_ {j}}}.}$

Dividir por no modifica la interpolación, pero produce ${\ Displaystyle L (x)}$${\ Displaystyle g (x)}$

${\ Displaystyle L (x) = {\ frac {\ sum _ {j = 0} ^ {k} {\ frac {w_ {j}} {x-x_ {j}}} y_ {j}} {\ sum _ {j = 0} ^ {k} {\ frac {w_ {j}} {x-x_ {j}}}}}}$

que se conoce como la segunda forma o forma verdadera de la fórmula de interpolación baricéntrica. Esta segunda forma tiene la ventaja de que no es necesario evaluarla para cada evaluación de . ${\ Displaystyle \ ell (x)}$${\ Displaystyle L (x)}$

Resto en la fórmula de interpolación de Lagrange

Al interpolar una función dada f por un polinomio de grado k en los nodos obtenemos el resto que se puede expresar como ${\ Displaystyle x_ {0}, ..., x_ {k}}$${\ Displaystyle R (x) = f (x) -L (x)}$

${\ Displaystyle R (x) = f [x_ {0}, \ ldots, x_ {k}, x] \ ell (x) = \ ell (x) {\ frac {f ^ {(k + 1)} ( \ xi)} {(k + 1)!}}, \ quad \ quad x_ {0} <\ xi <x_ {k},}$

donde es la notación para las diferencias divididas . Alternativamente, el resto se puede expresar como una integral de contorno en un dominio complejo como ${\ Displaystyle f [x_ {0}, \ ldots, x_ {k}, x]}$

${\ Displaystyle R (x) = {\ frac {\ ell (x)} {2 \ pi i}} \ int _ {C} {\ frac {f (t)} {(tx) (t-x_ {0 }) \ cdots (t-x_ {k})}} dt = {\ frac {\ ell (x)} {2 \ pi i}} \ int _ {C} {\ frac {f (t)} {( tx) \ ell (t)}} dt.}$

El resto se puede vincular como

${\ Displaystyle | R (x) | \ leq {\ frac {(x_ {k} -x_ {0}) ^ {k + 1}} {(k + 1)!}} \ max _ {x_ {0} \ leq \ xi \ leq x_ {k}} | f ^ {(k + 1)} (\ xi) |.}$

Derivación

Claramente, es cero en los nodos. Para encontrar en un punto , defina una nueva función y elija dónde está la constante que debemos determinar para un determinado . Elegimos para que tenga ceros (en todos los nodos y ) entre y (incluidos los puntos finales). Suponiendo que es -veces diferenciable, ya que y son polinomios y, por lo tanto, son infinitamente diferenciables, será -veces diferenciable. Según el teorema de Rolle , tiene ceros, tiene ceros ... tiene 1 cero, digamos . Escribiendo explícitamente : ${\ Displaystyle R (x)}$${\ Displaystyle R (x)}$${\ Displaystyle x_ {p}}$${\ Displaystyle F (x) = R (x) - {\ tilde {R}} (x) = f (x) -L (x) - {\ tilde {R}} (x)}$${\ textstyle {\ tilde {R}} (x) = C \ cdot \ prod _ {i = 0} ^ {k} (x-x_ {i})}$${\ Displaystyle C}$${\ Displaystyle x_ {p}}$${\ Displaystyle C}$${\ Displaystyle F (x)}$${\ Displaystyle k + 2}$${\ Displaystyle x_ {p}}$${\ Displaystyle x_ {0}}$${\ Displaystyle x_ {k}}$${\ Displaystyle f (x)}$${\ Displaystyle k + 1}$${\ Displaystyle L (x)}$${\ Displaystyle {\ tilde {R}} (x)}$${\ Displaystyle F (x)}$${\ Displaystyle k + 1}$${\ Displaystyle F ^ {(1)} (x)}$${\ Displaystyle k + 1}$${\ Displaystyle F ^ {(2)} (x)}$${\ Displaystyle k}$${\ Displaystyle F ^ {(k + 1)}}$${\ Displaystyle \ xi, \, x_ {0} <\ xi <x_ {k}}$${\ Displaystyle F ^ {(k + 1)} (\ xi)}$

${\ Displaystyle F ^ {(k + 1)} (\ xi) = f ^ {(k + 1)} (\ xi) -L ^ {(k + 1)} (\ xi) - {\ tilde {R }} ^ {(k + 1)} (\ xi)}$

${\ Displaystyle L ^ {(k + 1)} = 0, {\ tilde {R}} ^ {(k + 1)} = C \ cdot (k + 1)!}$(Porque el poder más alto de en es )${\ Displaystyle x}$${\ Displaystyle {\ tilde {R}} (x)}$${\ Displaystyle k + 1}$

${\ Displaystyle 0 = f ^ {(k + 1)} (\ xi) -C \ cdot (k + 1)!}$

La ecuación se puede reorganizar como

${\ Displaystyle C = {\ frac {f ^ {(k + 1)} (\ xi)} {(k + 1)!}}}$

Ya que tenemos${\ Displaystyle F (x_ {p}) = 0}$${\ Displaystyle R (x_ {p}) = {\ tilde {R}} (x_ {p}) = {\ frac {f ^ {k + 1} (\ xi)} {(k + 1)!}} \ prod _ {i = 0} ^ {k} (x_ {p} -x_ {i})}$

Derivados

Las derivadas th del polinomio de Lagrange se pueden escribir como ${\ Displaystyle d}$

${\ Displaystyle L ^ {(d)} (x): = \ sum _ {j = 0} ^ {k} y_ {j} \ ell _ {j} ^ {(d)} (x)}$.

Para la primera derivada, los coeficientes están dados por

${\ Displaystyle \ ell _ {j} ^ {(1)} (x): = \ sum _ {\ begin {smallmatrix} i = 0 \\ i \ not = j \ end {smallmatrix}} ^ {k} \ izquierda [{\ frac {1} {x_ {j} -x_ {i}}} \ prod _ {\ begin {smallmatrix} m = 0 \\ m \ not = (i, j) \ end {smallmatrix}} ^ {k} {\ frac {x-x_ {m}} {x_ {j} -x_ {m}}} \ right]}$

y para la segunda derivada

${\ Displaystyle \ ell _ {j} ^ {(2)} (x): = \ sum _ {\ begin {smallmatrix} i = 0 \\ i \ neq j \ end {smallmatrix}} ^ {k} {\ frac {1} {x_ {j} -x_ {i}}} \ left [\ sum _ {\ begin {smallmatrix} m = 0 \\ m \ neq (i, j) \ end {smallmatrix}} ^ {k } \ left ({\ frac {1} {x_ {j} -x_ {m}}} \ prod _ {\ begin {smallmatrix} l = 0 \\ l \ neq (i, j, m) \ end {smallmatrix }} ^ {k} {\ frac {x-x_ {l}} {x_ {j} -x_ {l}}} \ right) \ right]}$.

A través de la recursividad, se pueden calcular fórmulas para derivadas más altas.

Campos finitos

El polinomio de Lagrange también se puede calcular en campos finitos . Esto tiene aplicaciones en criptografía , como en el esquema de intercambio secreto de Shamir .

Ver también

• El algoritmo de Neville
• Forma de Newton del polinomio de interpolación
• Polinomio de Bernstein
• Teorema de carlson
• Constante de Lebesgue (interpolación)
• El sistema Chebfun
• Tabla de series newtonianas
• Covariante de Frobenius
• Fórmula de Sylvester
• Coeficiente de diferencia finita

Referencias

enlaces externos

• "Fórmula de interpolación de Lagrange" , Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• ALGLIB tiene implementaciones en C ++ / C # / VBA / Pascal.
• GSL tiene un código de interpolación polinomial en C
• SO tiene un ejemplo de MATLAB que demuestra el algoritmo y recrea la primera imagen de este artículo
• Método de interpolación de Lagrange: notas, PPT, Mathcad, Mathematica, MATLAB, Maple en el Instituto de métodos numéricos holísticos
• Polinomio de interpolación de Lagrange en www.math-linux.com
• Weisstein, Eric W. "Polinomio de interpolación de Lagrange" . MathWorld .
• Polinomio de Lagrange en ProofWiki
• Interpolación dinámica de Lagrange con JSXGraph
• Computación numérica con funciones: el proyecto Chebfun
• Función de hoja de cálculo de Excel para la interpolación bicúbica de Lagrange
• Polinomios de Lagrange en Python