Este artículo trata sobre los límites en la topología general. No debe confundirse con el
límite de una variedad .

Un conjunto (en azul claro) y su límite (en azul oscuro).
En la topología y las matemáticas en general, el límite de un subconjunto S de un espacio topológico X es el conjunto de puntos que pueden ser abordados tanto desde S y desde el exterior de S . Más precisamente, es el conjunto de puntos en el cierre de no pertenecer al interior de Un elemento del límite de se llama un punto límite de El término operación de límite se refiere a encontrar o tomar el límite de un conjunto. Las notaciones utilizadas para el límite de un conjunto incluyen y Algunos autores (por ejemplo, Willard, en Topología general ) utilizan el término frontera en lugar de límite en un intento de evitar la confusión con una definición diferente utilizada en la topología algebraica y la teoría de variedades . A pesar de la aceptación generalizada del significado de los términos límite y frontera, a veces se han utilizado para referirse a otros conjuntos. Por ejemplo, los espacios métricos por ET Copson utiliza el límite término para referirse a Hausdorff 's frontera , que se define como la intersección de un conjunto con su límite. Hausdorff también introdujo el término residuo , que se define como la intersección de un conjunto con el cierre del borde de su complemento.







Un componente conectado del límite de se llama componente de límite de

Definiciones comunes
Hay varias definiciones equivalentes para el límite de un subconjunto de un espacio topológico que se indicará o simplemente si se entiende:






- Es el cierre de menos el interior de en :




donde denota el cierre de in y denota el interior topológico de in





- Es la intersección del cierre de con el cierre de su complemento :


- Es el conjunto de puntos tal que cada vecindario de contiene al menos un punto de y al menos un punto no de :





Un punto límite de un conjunto se refiere a cualquier elemento del límite de ese conjunto. El límite definido anteriormente a veces se denomina límite topológico del conjunto para distinguirlo de otras nociones con nombres similares, como el límite de una variedad con límite o el límite de una variedad con esquinas , por nombrar solo algunos ejemplos.

Propiedades
El cierre de un conjunto es igual a la unión del conjunto con su límite:


donde denota el
cierre de en
Un conjunto está cerrado si y solo si contiene su límite, y abierto si y solo si está disjunto de su límite. El límite de un conjunto está cerrado ; esto se sigue de la fórmula que se expresa como la intersección de dos subconjuntos cerrados de





("Tricotomía")Dado cualquier subconjunto, cada punto de se encuentra exactamente en uno de los tres conjuntos y dicho de manera diferente,




y estos tres conjuntos están separados por pares . En consecuencia, si estos conjuntos no están vacíos, forman una partición de
Un punto es un punto límite de un conjunto si y solo si cada vecindario de contiene al menos un punto en el conjunto y al menos un punto que no está en el conjunto. Tanto el límite del interior de un conjunto como el límite del cierre de un conjunto están contenidos en el límite del conjunto.


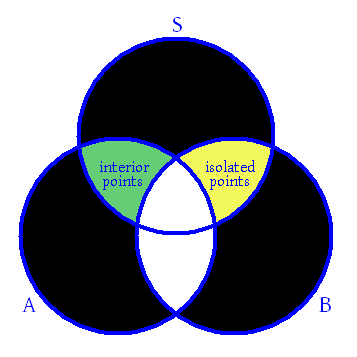
Diagrama de Venn conceptual que muestra las relaciones entre diferentes puntos de un subconjunto de = conjunto de puntos límite del conjunto de puntos límite del área sombreada en verde = conjunto de puntos interiores del área sombreada en amarillo = conjunto de puntos aislados de áreas sombreadas en negro = conjuntos vacíos. Cada punto de es un punto interior o un punto límite. Además, cada punto de es un punto de acumulación o un punto aislado. Asimismo, cada punto límite de es un punto de acumulación o un punto aislado. Los puntos aislados son siempre puntos límite.










Ejemplos de
Caracterizaciones y ejemplos generales
El límite de un conjunto es igual al límite del complemento del conjunto:

Si es un subconjunto abierto denso de entonces


El interior del límite de un conjunto cerrado es el conjunto vacío. En consecuencia, el interior del límite del cierre de un conjunto es el conjunto vacío. El interior del límite de un conjunto abierto es también el conjunto vacío. En consecuencia, el interior del límite del interior de un conjunto es el conjunto vacío. En particular, si es un subconjunto cerrado o abierto de entonces no existe ningún subconjunto no vacío tal que también sea un subconjunto abierto de
Este hecho es importante para la definición y uso de subconjuntos densos en ninguna parte , subconjuntos magros y espacios de Baire .





Un conjunto es el límite de algún conjunto abierto si y solo si está cerrado y no es denso en ninguna parte . El límite de un conjunto está vacío si y solo si el conjunto está cerrado y abierto (es decir, un conjunto cerrado ).
Ejemplos concretos
Considere la línea real con la topología habitual (es decir, la topología cuyos conjuntos de bases son intervalos abiertos ) y el subconjunto de números racionales (cuyo interior topológico en está vacío). Luego



![{\ estilo de visualización \ parcial (0,5) = \ parcial [0,5) = \ parcial (0,5] = \ parcial [0,5] = \ {0,5 \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84d5dd08b8ce4a5959c14f806036b74dda17723a)


![{\ estilo de visualización \ parcial (\ mathbb {Q} \ cap [0,1]) = [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/992baab3b186c92f1b758497f0437ae600af6c5c)
Estos dos últimos ejemplos ilustran el hecho de que el límite de un conjunto denso con interior vacío es su cierre. También muestran que es posible que el límite de un subconjunto contenga un subconjunto abierto no vacío de ; es decir, que el interior de in no esté vacío. Sin embargo, el límite de un subconjunto cerrado siempre tiene un interior vacío.





En el espacio de los números racionales con la topología habitual (la topología subespacial de ), el límite de where es irracional, está vacío.



El límite de un conjunto es una noción topológica y puede cambiar si se cambia la topología. Por ejemplo, dada la topología habitual en el límite de un disco cerrado es el círculo circundante del disco: si el disco se ve como un conjunto con su propia topología habitual, es decir, entonces el límite del disco es el propio disco: Si el disco se ve como su propio espacio topológico (con la topología subespacial de ), entonces el límite del disco está vacío.







Límite de una bola abierta frente a su esfera circundante
Este ejemplo demuestra que el límite topológico de una bola abierta de radio no es necesariamente igual a la correspondiente esfera de radio (centrada en el mismo punto); también muestra que el cierre de una bola abierta de radio no es necesariamente igual a la bola cerrada de radio (nuevamente centrada en el mismo punto). Denotar la habitual métrica euclidiana en por






que induce en la
topología euclidiana habitual . Vamos a denotar la unión del eje x con la unidad de círculo centrado en el origen ; es decir, que es un subespacio topológico de cuya topología es igual a la inducida por la (restricción de) la métrica
En particular, los conjuntos y son todos los subconjuntos cerrados de y subconjuntos por lo tanto también cerradas de su subespacio
De aquí en adelante, a menos que claramente se indique lo contrario , se debe suponer que cada bola abierta, bola cerrada y esfera está centrada en el origen y, además, solo se considerará el espacio métrico (y no su superespacio ); siendo este un camino conectados y trayectoria-conectado localmente espacio métrico completo .










![{\ Displaystyle \ {0 \} \ times [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a3278f4a9ff634e32edeb1039a7687ef077566e)





Denote la bola abierta de radio adentro de
modo que cuando luego





es el subintervalo abierto del eje-estrictamente entre y
La esfera unitaria en ("unidad" significa que su radio es ) es






mientras que la bola unitaria cerrada hacia adentro es la unión de la bola unitaria abierta y la esfera unitaria centrada en este mismo punto:

![{\ Displaystyle \ left \ {p \ in X: d (p, \ mathbf {0}) \ leq 1 \ right \} = S ^ {1} \ cup \ left (\ {0 \} \ times [-1 , 1] \ derecha).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbbdb5bb903d77c3b2b46a464186540e9f2146ed)
Sin embargo, la frontera topológica de cierre y topológica en la bola unidad abierta son:




![{\ Displaystyle \ partial _ {X} B_ {1} = \ {(0,1), (0, -1) \} \ quad {\ text {y}} \ quad \ operatorname {cl} _ {X} B_ {1} ~ = ~ B_ {1} \ taza \ parcial _ {X} B_ {1} ~ = ~ B_ {1} \ taza \ {(0,1), (0, -1) \} ~ = ~ \ {0 \} \ times [-1,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2df64b6756937f1c40bb722992413fe99c747e7b)
En particular, el límite topológico de la bola unitaria abierta es un subconjunto adecuado de la esfera unitaria en
Y el cierre topológico de la bola unitaria abierta es un subconjunto adecuado de la bola unitaria cerrada en
El punto, por ejemplo, no puede pertenecer porque no existe una secuencia en que converge a ella; el mismo razonamiento se generaliza para explicar también por qué ningún punto fuera del subintervalo cerrado pertenece a Debido a que el límite topológico del conjunto es siempre un subconjunto de la clausura de, se deduce que también debe ser un subconjunto de



![{\ Displaystyle \ left \ {p \ in X: d (p, \ mathbf {0}) \ leq 1 \ right \} = S ^ {1} \ cup \ left (\ {0 \} \ times [-1 , 1] \ right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84ca278fa188aca7582438f63a8eb555344f5719)





![{\ Displaystyle \ {0 \} \ times [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a3278f4a9ff634e32edeb1039a7687ef077566e)




![{\ Displaystyle \ {0 \} \ times [-1,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50bd9bfe3c9b6013059a0365209b818ee5b8d406)
En cualquier espacio métrico, el límite topológico de una bola abierta de radio centrada en un punto es siempre un subconjunto de la esfera de radio centrada en ese mismo punto ; es decir,







siempre aguanta.
Además, la esfera unitaria en contiene, que es un subconjunto abierto de Esto muestra, en particular, que la esfera unitaria en contiene un subconjunto
abierto no vacío de





Límite de un límite
Para cualquier conjunto, donde denota el
superconjunto con igualdad si y solo si el límite de no tiene puntos interiores, que será el caso, por ejemplo, si está cerrado o abierto. Dado que el límite de un conjunto es cerrado, para cualquier conjunto, el operador de límite satisface un tipo debilitado de idempotencia .






Al discutir los límites de las variedades o símplex y sus complejos simpliciales , uno a menudo se encuentra con la afirmación de que el límite de la frontera siempre está vacío. De hecho, la construcción de la homología singular se basa críticamente en este hecho. La explicación de la aparente incongruencia es que el límite topológico (el tema de este artículo) es un concepto ligeramente diferente del límite de una variedad o de un complejo simplicial. Por ejemplo, el límite de un disco abierto visto como una variedad está vacío, al igual que su límite topológico visto como un subconjunto de sí mismo, mientras que su límite topológico visto como un subconjunto del plano real es el círculo que rodea al disco. Por el contrario, el límite de un disco cerrado visto como una variedad es el círculo delimitador, al igual que su límite topológico visto como un subconjunto del plano real, mientras que su límite topológico visto como un subconjunto de sí mismo está vacío. En particular, el límite topológico depende del espacio ambiental, mientras que el límite de una variedad es invariante.
Ver también
Notas
Citas
Referencias






































![{\ estilo de visualización \ parcial (0,5) = \ parcial [0,5) = \ parcial (0,5] = \ parcial [0,5] = \ {0,5 \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84d5dd08b8ce4a5959c14f806036b74dda17723a)


![{\ estilo de visualización \ parcial (\ mathbb {Q} \ cap [0,1]) = [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/992baab3b186c92f1b758497f0437ae600af6c5c)





















![{\ Displaystyle \ {0 \} \ times [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a3278f4a9ff634e32edeb1039a7687ef077566e)









![{\ Displaystyle \ left \ {p \ in X: d (p, \ mathbf {0}) \ leq 1 \ right \} = S ^ {1} \ cup \ left (\ {0 \} \ times [-1 , 1] \ derecha).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbbdb5bb903d77c3b2b46a464186540e9f2146ed)



![{\ Displaystyle \ partial _ {X} B_ {1} = \ {(0,1), (0, -1) \} \ quad {\ text {y}} \ quad \ operatorname {cl} _ {X} B_ {1} ~ = ~ B_ {1} \ taza \ parcial _ {X} B_ {1} ~ = ~ B_ {1} \ taza \ {(0,1), (0, -1) \} ~ = ~ \ {0 \} \ times [-1,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2df64b6756937f1c40bb722992413fe99c747e7b)



![{\ Displaystyle \ left \ {p \ in X: d (p, \ mathbf {0}) \ leq 1 \ right \} = S ^ {1} \ cup \ left (\ {0 \} \ times [-1 , 1] \ right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84ca278fa188aca7582438f63a8eb555344f5719)


![{\ Displaystyle \ {0 \} \ times [-1,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50bd9bfe3c9b6013059a0365209b818ee5b8d406)









