Algoritmo binario GCD - Binary GCD algorithm

Visualización del uso del algoritmo binario GCD para encontrar el máximo común divisor (MCD) de 36 y 24. Por lo tanto, el MCD es 2 ² × 3 = 12.

El algoritmo binario GCD , también conocido como algoritmo de Stein o el algoritmo binario euclidiano , es un algoritmo que calcula el máximo común divisor de dos enteros no negativos. El algoritmo de Stein usa operaciones aritméticas más simples que el algoritmo euclidiano convencional ; reemplaza la división con cambios aritméticos , comparaciones y restas.

Aunque el algoritmo en su forma contemporánea fue publicado por primera vez por el físico y programador israelí Josef Stein en 1967, puede haber sido conocido en el siglo II a. C., en la antigua China.

Algoritmo

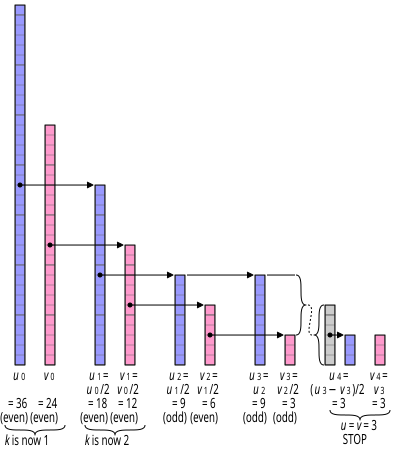
El algoritmo reduce el problema de encontrar el MCD de dos números no negativos v y u aplicando repetidamente estas identidades:

• mcd (0, v ) = v , porque todo divide a cero y v es el número más grande que divide a v . De manera similar, mcd ( u , 0) =  u .
• mcd ( 2u ,  2v ) = 2 · mcd ( u , v )
• mcd ( 2u ,  v ) = mcd ( u ,  v ), si v es impar (2 no es un divisor común). De manera similar, mcd ( u ,  2v ) = mcd ( u ,  v ) si u es impar.
• mcd ( u ,  v ) = mcd (| u  -  v |, min ( u , v )), si tanto u como v son impares.

Implementación

Si bien la descripción anterior del algoritmo es matemáticamente correcta, las implementaciones de software de alto rendimiento suelen diferir de él en algunas formas notables:

• evitar la división de prueba por 2 a favor de un desplazamiento de bits único y la primitiva de contar ceros finales ; esto es funcionalmente equivalente a aplicar repetidamente la identidad 3, pero mucho más rápido;
• expresando el algoritmo de manera iterativa en lugar de recursiva : la implementación resultante se puede diseñar para evitar el trabajo repetido, invocando la identidad 2 al inicio y manteniendo como invariante que ambos números son impares al ingresar al ciclo, que solo necesita implementar las identidades 3 y 4;
• hacer que el cuerpo del bucle no tenga ramificaciones excepto por su condición de salida ( v == 0 ): en el siguiente ejemplo, el intercambio de u y v (asegurando que u ≤ v ) se compila en movimientos condicionales ; Las ramas difíciles de predecir pueden tener un gran impacto negativo en el rendimiento.

A continuación se muestra una implementación del algoritmo en Rust que ejemplifica esas diferencias, adaptado de uutils :

pub fn gcd(mut u: u64, mut v: u64) -> u64 {
    use std::cmp::min;
    use std::mem::swap;

    // Base cases: gcd(n, 0) = gcd(0, n) = n
    if u == 0 {
        return v;
    } else if v == 0 {
        return u;
    }

    // Using identities 2 and 3:
    // gcd(2ⁱ u, 2ʲ v) = 2ᵏ gcd(u, v) with u, v odd and k = min(i, j)
    // 2ᵏ is the greatest power of two that divides both u and v
    let i = u.trailing_zeros();  u >>= i;
    let j = v.trailing_zeros();  v >>= j;
    let k = min(i, j);

    loop {
        // u and v are odd at the start of the loop
        debug_assert!(u % 2 == 1, "u = {} is even", u);
        debug_assert!(v % 2 == 1, "v = {} is even", v);

        // Swap if necessary so u <= v
        if u > v {
            swap(&mut u, &mut v);
        }

        // Using identity 4 (gcd(u, v) = gcd(|v-u|, min(u, v))
        v -= u;

        // Identity 1: gcd(u, 0) = u
        // The shift by k is necessary to add back the 2ᵏ factor that was removed before the loop
        if v == 0 {
            return u << k;
        }

        // Identity 3: gcd(u, 2ʲ v) = gcd(u, v) (u is known to be odd)
        v >>= v.trailing_zeros();
    }
}

Eficiencia

El algoritmo requiere O ( n ) pasos, donde n es el número de bits en el mayor de los dos números, ya que cada 2 pasos reduce al menos uno de los operandos en al menos un factor de 2. Cada paso implica solo unas pocas operaciones aritméticas. operaciones (O (1) con una pequeña constante); cuando se trabaja con números del tamaño de una palabra , cada operación aritmética se traduce en una sola operación de máquina, por lo que el número de operaciones de la máquina es del orden de log₂ (max ( u , v )), es decir, n .

Sin embargo, la complejidad asintótica de este algoritmo es O (n ² ), ya que esas operaciones aritméticas (restar y desplazar) toman cada una un tiempo lineal para números de tamaño arbitrario (una operación de máquina por palabra de la representación). Esto es lo mismo que para el algoritmo euclidiano, aunque un análisis más preciso de Akhavi y Vallée demostró que el GCD binario usa aproximadamente un 60% menos de operaciones de bits.

Extensiones

El algoritmo binario de GCD se puede ampliar de varias formas, ya sea para generar información adicional, tratar con números enteros arbitrariamente grandes de manera más eficiente o para calcular GCD en dominios distintos de los enteros.

El extendida binario GCD algoritmo, análogo al algoritmo de Euclides extendido , se ajusta en el primer tipo de extensión, ya que proporciona los coeficientes de Bézout además de la GCD, es decir, números enteros una y b tales que a · u + b · v = gcd ( u , v ).

En el caso de números enteros grandes, la mejor complejidad asintótica es O (log n M ( n )), siendo M ( n ) el costo de la multiplicación de n bits; esto es casi lineal y mucho más pequeño que el O (n ² ) del algoritmo binario GCD, aunque las implementaciones concretas solo superan a los algoritmos más antiguos para números mayores de aproximadamente 64 kilobits ( es decir, mayores de 8 × 10 ¹⁹²⁶⁵ ). Esto se logra extendiendo el algoritmo binario GCD usando ideas del algoritmo de Schönhage-Strassen para la multiplicación rápida de enteros.

El algoritmo binario GCD también se ha extendido a dominios distintos de los números naturales, como enteros gaussianos , enteros de Eisenstein , anillos cuadráticos y dominios de factorización únicos arbitrarios .

Descripción histórica

En la antigua China, bajo la dinastía Han , se conocía un algoritmo para calcular el GCD de dos números como método para reducir fracciones:

Si es posible, córtelo por la mitad; de lo contrario, tome el denominador y el numerador, reste el menor del mayor y hágalo alternativamente para que sean iguales. Reducir por el mismo número.

-  Fangtian - Agrimensura, los nueve capítulos sobre el arte matemático

La frase "si es posible, reducir a la mitad" es ambigua,

• si esto se aplica cuando cualquiera de los números se vuelve par, el algoritmo es el algoritmo binario GCD;
• si esto solo se aplica cuando ambos números son pares, el algoritmo es similar al algoritmo euclidiano .

Ver también

• Algoritmo euclidiano
• Algoritmo euclidiano extendido
• Minimo común multiplo

Referencias

Otras lecturas

• Knuth, Donald (1998). "§4.5 Aritmética racional". Algoritmos seminuméricos . El arte de la programación informática . 2 (3ª ed.). Addison-Wesley. págs. 330–417. ISBN 978-0-201-89684-8.

Cubre el GCD binario extendido y un análisis probabilístico del algoritmo.

• Cohen, Henri (1993). "Capítulo 1: Algoritmos fundamentales de teoría de números". Un curso de teoría de números algebraicos computacionales . Textos de Posgrado en Matemáticas . 138 . Springer-Verlag . págs. 12-24. ISBN 0-387-55640-0.

Cubre una variedad de temas, incluido el algoritmo GCD binario extendido que genera coeficientes de Bézout , manejo eficiente de enteros de precisión múltiple usando una variante del algoritmo GCD de Lehmer y la relación entre GCD y expansiones de fracciones continuas de números reales.

• Vallée, Brigitte (septiembre-octubre de 1998). "Dinámica del algoritmo binario euclidiano: análisis funcionales y operadores" . Algoritmica . 22 (4): 660–685. doi : 10.1007 / PL00009246 . S2CID  27441335 . Archivado desde el original (PS) el 13 de mayo de 2011.Mantenimiento CS1: formato de fecha ( enlace )

Un análisis del algoritmo en el caso promedio, a través de la lente del análisis funcional : los parámetros principales de los algoritmos se proyectan como un sistema dinámico , y su valor promedio está relacionado con la medida invariante del operador de transferencia del sistema .

enlaces externos

• Diccionario NIST de algoritmos y estructuras de datos: algoritmo binario GCD
• Cortar el nudo: algoritmo binario de Euclides al cortar el nudo
• Análisis del algoritmo binario euclidiano (1976), un artículo de Richard P. Brent , que incluye una variante que usa desplazamientos a la izquierda