Sólido de Arquímedes - Archimedean solid
En geometría , un sólido de Arquímedes es uno de los 13 sólidos enumerados por primera vez por Arquímedes . Son los poliedros uniformes convexos compuestos por polígonos regulares que se encuentran en vértices idénticos , excluyendo los cinco sólidos platónicos (que están compuestos por un solo tipo de polígono) y excluyendo los prismas y antiprismas . Se diferencian de los sólidos de Johnson , cuyas caras poligonales regulares no se encuentran en vértices idénticos.
"Vértices idénticos" significa que cada dos vértices son simétricos entre sí: una isometría global de todo el sólido lleva un vértice al otro mientras coloca el sólido directamente en su posición inicial. Branko Grünbaum ( 2009 ) observó que un poliedro 14, la gyrobicupla cuadrada alargada (o pseudo-rombicuboctaedro), cumple con una definición más débil de un sólido de Arquímedes, en el que "vértices idénticos" significa simplemente que las caras que rodean cada vértice son del mismo tipo (es decir, cada vértice se ve igual de cerca), por lo que solo se requiere una isometría local. Grünbaum señaló un error frecuente en el que los autores definen los sólidos de Arquímedes utilizando esta definición local, pero omiten el poliedro 14. Si solo se enumeran 13 poliedros, la definición debe usar simetrías globales del poliedro en lugar de vecindarios locales.
Los prismas y antiprismas , cuyos grupos de simetría son los diédricos , generalmente no se consideran sólidos de Arquímedes, aunque sus caras son polígonos regulares y sus grupos de simetría actúan de manera transitiva sobre sus vértices. Excluyendo estas dos familias infinitas, hay 13 sólidos de Arquímedes. Todos los sólidos de Arquímedes (pero no la girobicúpula cuadrada alargada) se pueden hacer mediante construcciones de Wythoff a partir de los sólidos platónicos con simetría tetraédrica , octaédrica e icosaédrica .
Origen del nombre
Los sólidos de Arquímedes toman su nombre de Arquímedes , quien los discutió en una obra ahora perdida. Pappus se refiere a él, afirmando que Arquímedes enumeró 13 poliedros. Durante el Renacimiento , los artistas y matemáticos valoraban las formas puras con alta simetría, y hacia 1620 Johannes Kepler había completado el redescubrimiento de los 13 poliedros, además de definir los prismas , antiprismas y los sólidos no convexos conocidos como poliedros de Kepler-Poinsot. . (Consulte Schreiber, Fischer & Sternath 2008 para obtener más información sobre el redescubrimiento de los sólidos de Arquímedes durante el renacimiento).
Kepler también pudo haber encontrado la gyrobicupla cuadrada alargada (pseudorhombicuboctahedron): al menos, una vez afirmó que había 14 sólidos de Arquímedes. Sin embargo, su enumeración publicada solo incluye los 13 poliedros uniformes, y la primera declaración clara de la existencia del pseudorhombicuboctahedron fue hecha en 1905, por Duncan Sommerville .
Clasificación
Hay 13 sólidos de Arquímedes (sin contar la girobicúpula cuadrada alargada ; 15 si las imágenes especulares de dos enantiomorfos , el cubo chato y el dodecaedro chato, se cuentan por separado).
Aquí, la configuración de vértices se refiere al tipo de polígonos regulares que se encuentran en cualquier vértice dado. Por ejemplo, una configuración de vértice de (4,6,8) significa que un cuadrado , un hexágono y un octágono se encuentran en un vértice (tomando el orden en el sentido de las agujas del reloj alrededor del vértice).
| Nombre / (nombre alternativo) |
Schläfli Coxeter |
Transparente | Sólido | Neto | Vértice conf. / fig. |
Caras | Bordes | Vert. | Volumen (bordes de la unidad) |
Grupo de puntos |
Esfericidad | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| tetraedro truncado | t {3,3} |
 |

|
|
3.6.6
|
8 | 4 triángulos 4 hexágonos |
18 | 12 | 2.710 576 | T d | 0,775 4132 |
|
cuboctaedro (rombitetratetraedro, girobicúpula triangular) |
r {4,3} o rr {3,3} |
 |

|

|
3.4.3.4
|
14 | 8 triángulos 6 cuadrados |
24 | 12 | 2.357 023 | O h | 0,904 9972 |
| cubo truncado | t {4,3} |
 |

|
|
3.8.8
|
14 | 8 triángulos 6 octágonos |
36 | 24 | 13.599 663 | O h | 0,849 4937 |
|
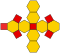
octaedro truncado (tetraedro truncado) |
t {3,4} o tr {3,3} |
 |

|
|
4.6.6
|
14 | 6 cuadrados 8 hexágonos |
36 | 24 | 11.313 709 | O h | 0,909 9178 |
|
rombicuboctaedro (pequeño rombicuboctaedro, ortobicúpula cuadrada alargada) |
rr {4,3} |
 |

|
|
3.4.4.4
|
26 | 8 triángulos 18 cuadrados |
48 | 24 | 8.714 045 | O h | 0,954 0796 |
|
cuboctaedro truncado (gran rombicuboctaedro) |
tr {4,3} |
 |

|
|
4.6.8
|
26 | 12 cuadrados 8 hexágonos 6 octágonos |
72 | 48 | 41.798 990 | O h | 0,943 1657 |
|
cubo de desaire (cuboctaedro de desaire) |
sr {4,3} |
 |

|
|
3.3.3.3.4
|
38 | 32 triángulos 6 cuadrados |
60 | 24 | 7.889 295 | O | 0,965 1814 |
|
icosidodecaedro (gyrobirotunda pentagonal) |
r {5,3} |
 |

|
|
3.5.3.5
|
32 | 20 triángulos 12 pentágonos |
60 | 30 | 13.835 526 | Yo h | 0,951 0243 |
| dodecaedro truncado | t {5,3} |
 |

|
|
3.10.10
|
32 | 20 triángulos 12 decágonos |
90 | 60 | 85.039 665 | Yo h | 0,926 0,125 |
| icosaedro truncado | t {3,5} |
 |

|
|
5.6.6
|
32 | 12 pentágonos 20 hexágonos |
90 | 60 | 55.287 731 | Yo h | 0,966 6219 |
|
rombicosidodecaedro (pequeño rombicosidodecaedro) |
rr {5,3} |
 |

|
|
3.4.5.4
|
62 | 20 triángulos 30 cuadrados 12 pentágonos |
120 | 60 | 41.615 324 | Yo h | 0,979 2370 |
|
icosidodecaedro truncado (gran rombicosidodecaedro) |
tr {5,3} |
 |

|
|
4.6.10
|
62 | 30 cuadrados 20 hexágonos 12 decágonos |
180 | 120 | 206.803 399 | Yo h | 0,970 3127 |
|
dodecaedro chato (icosidodecaedro chato) |
sr {5,3} |
 |

|
|
3.3.3.3.5
|
92 | 80 triángulos 12 pentágonos |
150 | 60 | 37.616 650 | I | 0,982 0,114 |
Algunas definiciones de poliedro semirregular incluyen una figura más, la girobicúpula cuadrada alargada o "pseudo-rombicuboctaedro".
Propiedades
El número de vértices es 720 ° dividido por el defecto del ángulo del vértice .
El cuboctaedro y el icosidodecaedro tienen bordes uniformes y se denominan cuasi regulares .
Los duales de los sólidos de Arquímedes se denominan sólidos catalanes . Junto con las bipirámides y trapezoedros , estos son los sólidos de caras uniformes con vértices regulares.
Quiralidad
El cubo chato y el dodecaedro chato se conocen como quirales , ya que vienen en forma zurda (latín: levomorfo o laevomorfo) y forma diestra (latín: dextromorfo). Cuando algo viene en múltiples formas que son la imagen de espejo tridimensional del otro , estas formas pueden llamarse enantiomorfos. (Esta nomenclatura también se usa para las formas de ciertos compuestos químicos ).
Construcción de sólidos de Arquímedes

Los diferentes sólidos de Arquímedes y Platónicos se pueden relacionar entre sí utilizando un puñado de construcciones generales. Comenzando con un sólido platónico, el truncamiento implica cortar esquinas. Para preservar la simetría, el corte se realiza en un plano perpendicular a la línea que une una esquina al centro del poliedro y es el mismo para todas las esquinas. Dependiendo de cuánto se trunca (ver tabla a continuación), se pueden crear diferentes sólidos platónicos y arquimedianos (y otros). Si el truncamiento es exactamente lo suficientemente profundo como para que cada par de caras de vértices adyacentes comparta exactamente un punto, se conoce como rectificación. Una expansión , o cantelación , implica alejar cada cara del centro (la misma distancia para preservar la simetría del sólido platónico) y tomar el casco convexo. La expansión con torsión también implica rotar las caras, dividiendo así cada rectángulo correspondiente a un borde en dos triángulos por una de las diagonales del rectángulo. La última construcción que usamos aquí es el truncamiento de las esquinas y los bordes. Ignorando la escala, la expansión también se puede ver en la rectificación de la rectificación. Asimismo, el cantitruncation puede verse como el truncamiento de la rectificación.
| Simetría |
Tetraédrico
|
Octaédrico
|
Icosaédrico
|
|||
|---|---|---|---|---|---|---|
| Comenzando una operación sólida |
Símbolo {p, q} |
Tetraedro {3,3} 
|
Cubo {4,3} |
Octaedro {3,4} 
|
Dodecaedro {5,3} 
|
Icosaedro {3,5} 
|
| Truncamiento (t) | t {p, q} |
tetraedro truncado
|
cubo truncado
|
octaedro truncado |
dodecaedro truncado
|
icosaedro truncado
|
|
Rectificación (r) Ambo (a) |
r {p, q} |
tetraedro (octaedro) |
cuboctaedro |
icosidodecaedro
|
||
|
Bitruncation (2t) Dual kis (dk) |
2t {p, q} |
tetraedro truncado |
octaedro truncado
|
cubo truncado
|
icosaedro truncado
|
dodecaedro truncado
|
|
Birectificación (2r) Dual (d) |
2r {p, q} |
tetraedro |
octaedro
|
cubo |
icosaedro
|
dodecaedro
|
|
cantelación (rr) Expansión (e) |
rr {p, q} |
rombitetratetraedro (cuboctaedro) 
|
rombicuboctaedro
|
rombicosidodecaedro 
|
||
| Snub rectificado (sr) Snub (s) |
sr {p, q} |
tetratetraedro chato (icosaedro) |
cuboctaedro chato
|
icosidodecaedro desaire
|
||
|
Cantitruncation (tr) Bisel (b) |
tr {p, q} |
tetraedro truncado (octaedro truncado) 
|
cuboctaedro truncado |
icosidodecaedro truncado
|
||
Nótese la dualidad entre el cubo y el octaedro, y entre el dodecaedro y el icosaedro. Además, en parte porque el tetraedro es auto-dual, solo un sólido de Arquímedes que tiene como mucho simetría tetraédrica. (Todos los sólidos platónicos tienen al menos simetría tetraédrica, ya que la simetría tetraédrica es una operación de simetría de (es decir, está incluida en) simetrías octaédricas e isoédricas, lo cual se demuestra por el hecho de que un octaedro puede verse como un tetraedro rectificado, y un icosaedro puede ser utilizado como un tetraedro chato.)
Proyección estereográfica
| tetraedro truncado | cubo truncado | octaedro truncado | dodecaedro truncado | icosaedro truncado | |||||
|---|---|---|---|---|---|---|---|---|---|
 centrado en triangulo |
 centrado en hexágono |
 centrado en el octágono |
 centrado en triangulo |
 centrado en el cuadrado |
 centrado en hexágono |
 Centrado en decágono |
 Centrado en el triángulo |
 centrado en el pentágono |
 centrado en hexágono |
| cuboctaedro | icosidodecaedro | rombicuboctaedro | rombicosidodecaedro | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 centrado en el cuadrado |
 centrado en triangulo |
 centrado en el vértice |
 centrado en el pentágono |
 centrado en triangulo |
 centrado en el cuadrado |
 centrado en el cuadrado |
 centrado en triangulo |
 Centrado en el Pentágono |
 Centrado en el triángulo |
 Centrado en el cuadrado |
|||
| cuboctaedro truncado | icosidodecaedro truncado | cubo de desaire | ||||
|---|---|---|---|---|---|---|
 centrado en el cuadrado |
 centrado en hexágono |
 centrado en el octágono |

|

|
|
 centrado en el cuadrado |
Ver también
- Azulejos aperiódicos
- Gráfico de Arquímedes
- Gemelos icosaédricos
- Lista de poliedros uniformes
- Cubo de Prince Rupert # Generalizaciones
- Cuasicristal
- Poliedro regular
- Poliedro semirregular
- Poliedro toroidal
- Poliedro uniforme
Citas
Referencias generales
- Grünbaum, Branko (2009), "An perdurable error", Elemente der Mathematik , 64 (3): 89–101, doi : 10.4171 / EM / 120 , MR 2520469. Reimpreso en Pitici, Mircea, ed. (2011), The Best Writing on Mathematics 2010 , Princeton University Press, págs. 18–31.
- Jayatilake, Udaya (marzo de 2005). "Cálculos sobre poliedros regulares de caras y vértices". Gaceta matemática . 89 (514): 76–81. doi : 10.1017 / S0025557200176818 . S2CID 125675814 ..
- Malkevitch, Joseph (1988), "Hitos en la historia de los poliedros", en Senechal, M .; Fleck, G. (eds.), Dar forma al espacio: un enfoque poliédrico , Boston: Birkhäuser, págs. 80–92.
- Pugh, Anthony (1976). Poliedros: un enfoque visual . California: Universidad de California Press Berkeley. ISBN 0-520-03056-7. Capitulo 2
- Williams, Robert (1979). La base geométrica de la estructura natural: un libro fuente de diseño . Publicaciones de Dover, Inc. ISBN 0-486-23729-X. (Sección 3-9)
- Schreiber, Peter; Fischer, Gisela; Sternath, Maria Luise (2008). "Nueva luz sobre el redescubrimiento de los sólidos de Arquímedes durante el renacimiento". Archivo de Historia de las Ciencias Exactas . 62 (4): 457–467. Código Bibliográfico : 2008AHES ... 62..457S . doi : 10.1007 / s00407-008-0024-z . ISSN 0003-9519 . S2CID 122216140 ..
enlaces externos
- Weisstein, Eric W. "Arquímedes sólido" . MathWorld .
- Sólidos de Arquímedes por Eric W. Weisstein , Proyecto de demostraciones Wolfram .
- Modelos en papel de sólidos de Arquímedes y sólidos catalanes
- Modelos de papel gratis (redes) de sólidos de Arquímedes
- Los poliedros uniformes por el Dr. R. Mäder
- Sólidos de Arquímedes en poliedros visuales por David I. McCooey
- Poliedros de realidad virtual , la enciclopedia de poliedros de George W. Hart
- Penúltimo origami modular de James S. Plank
- Poliedros 3D interactivos en Java
- Solid Body Viewer es un visor de poliedros 3D interactivo que le permite guardar el modelo en formato svg, stl u obj.
- Stella: Polyhedron Navigator : software utilizado para crear muchas de las imágenes de esta página.
- Modelos en papel de poliedros de Arquímedes (y otros)





