Subgrupo - Subgroup

Estructura algebraica → Teoría de grupos Teoría de grupos
Nociones basicas Subgrupo Subgrupo normal Grupo cociente Producto (semi) directo Homomorfismos de grupo núcleo imagen suma directa producto de corona sencillo finito infinito continuo multiplicativo aditivo cíclico abeliano diedro nilpotente soluble acción Glosario de teoría de grupos Lista de temas de teoría de grupos
Grupos finitos Clasificación de grupos simples finitos cíclico alterno Tipo de mentira esporádico Teorema de Cauchy Teorema de lagrange Teoremas de Sylow Teorema de Hall grupo p Grupo abeliano elemental Grupo Frobenius Multiplicador de Schur Grupo simétrico S n Klein de cuatro grupos V Grupo diedro D n Grupo de cuaterniones Q Grupo dicíclico Dic n
Grupos discretos Celosías Enteros ( )${\ Displaystyle \ mathbb {Z}}$ Grupo libre Grupos modulares PSL (2, )${\ Displaystyle \ mathbb {Z}}$ SL (2, )${\ Displaystyle \ mathbb {Z}}$ Grupo aritmético Enrejado Grupo hiperbólico
Grupos topológicos y de mentira Solenoide Circulo GL lineal general ( n ) SL lineal especial ( n ) Ortogonal O ( n ) Euclidiana E ( n ) SO ortogonal especial ( n ) Unitario U ( n ) SU unitario especial ( n ) Simpléctica Sp ( n ) G 2 F 4 E 6 E 7 E 8 Lorentz Poincaré Conformal Difeomorfismo Círculo Grupo de mentiras de dimensión infinita O (∞) SU (∞) Sp (∞)
Grupos algebraicos Grupo algebraico lineal Grupo reductivo Variedad abeliana Curva elíptica
v t mi

En la teoría de grupos , una rama de las matemáticas , dado un grupo G bajo una operación binaria  ∗, un subconjunto H de G se llama subgrupo de G si H también forma un grupo bajo la operación ∗. Más precisamente, H es un subgrupo de G si la restricción de * a H × H es una operación de grupo en H . Esto generalmente se denota H ≤ G , leído como " H es un subgrupo de G ".

El subgrupo trivial de cualquier grupo es el subgrupo { e } que consiste solo en el elemento de identidad.

Un subgrupo adecuado de un grupo G es un subgrupo H que es un subconjunto adecuado de G (es decir, H ≠ G ). Esto generalmente se representa en forma de notación por H < G , leído como " H es un subgrupo adecuado de G ". Algunos autores también excluyen al grupo trivial de ser apropiado (es decir, H ≠ { e }).

Si H es un subgrupo de G , entonces G es a veces llamado un overgroup de H .

Las mismas definiciones se aplican de manera más general cuando G es un semigrupo arbitrario , pero este artículo solo se ocupará de subgrupos de grupos. El grupo G a veces se denota por el par ordenado ( G , ∗) , generalmente para enfatizar la operación ∗ cuando G tiene múltiples estructuras algebraicas u otras.

Propiedades básicas de los subgrupos

• Un subconjunto H del grupo G es un subgrupo de G si y solo si no está vacío y está cerrado bajo productos e inversos. (Las condiciones de cierre significan lo siguiente: siempre que un y b son en H , entonces ab y un ^-1 están también en H Estas dos condiciones se pueden combinar en una condición equivalente:. Cada vez que un y b son en H , entonces ab ^-1 también está en H. ) En el caso de que H sea ​​finito, entonces H es un subgrupo si y solo si H está cerrado bajo productos. (En este caso, cada elemento a de H genera un subgrupo cíclico finito de H , y la inversa de a es entonces a ⁻¹ = a ^{n −1} , donde n es el orden de a ).
• La condición anterior se puede establecer en términos de un homomorfismo ; es decir, H es un subgrupo de un grupo G si y sólo si H es un subconjunto de G y hay un homomorfismo de inclusión (es decir, i ( un ) = una para cada una ) a partir de H a G .
• La identidad de un subgrupo es la identidad del grupo: si G es un grupo con la identidad e _G , y H es un subgrupo de G con la identidad e _H , a continuación, e _H = e _G .
• El inverso de un elemento en un subgrupo es el inverso del elemento en el grupo: Si H es un subgrupo de un grupo G , y un y b son elementos de H tal que ab = ba = e _H , entonces ab = ba = e _G .
• La intersección de los subgrupos A y B es nuevamente un subgrupo. La unión de los subgrupos A y B es un subgrupo si y solo si A o B contienen al otro, ya que, por ejemplo, 2 y 3 están en la unión de 2Z y 3Z pero su suma 5 no lo es. Otro ejemplo es la unión del eje xy el eje y en el plano (con la operación de suma); cada uno de estos objetos es un subgrupo, pero su unión no lo es. Esto también sirve como ejemplo de dos subgrupos, cuya intersección es precisamente la identidad.
• Si S es un subconjunto de G , entonces existe un subgrupo mínimo que contiene S , que se puede encontrar tomando la intersección de todos los subgrupos que contienen S ; se denota por ⟨ S ⟩ y se dice que es el subgrupo generado por S . Un elemento de G está en ⟨ S ⟩ si y sólo si es un producto finito de elementos de S y sus inversos.
• Cada elemento de una de un grupo G genera el subgrupo cíclico ⟨ un ⟩. Si ⟨ un ⟩ es isomorfo a Z / n Z para algún entero positivo n , entonces n es el número entero positivo más pequeño para el que un ⁿ = e , y n se llama el orden de una . Si ⟨ un ⟩ es isomorfo a Z , entonces una se dice que tiene orden infinito .
• Los subgrupos de cualquier grupo dado forman un entramado completo bajo inclusión, llamado entramado de subgrupos . (Si bien aquí el mínimo es la intersección habitual de la teoría de conjuntos, el superior de un conjunto de subgrupos es el subgrupo generado por la unión de la teoría de conjuntos de los subgrupos, no la unión de la teoría de conjuntos en sí). Si e es la identidad de G , entonces el grupo trivial { e } es el mínimo subgrupo de G , mientras que el máximo subgrupo es el grupo G en sí.

Cosets y el teorema de Lagrange

Dado un subgrupo H y algo de a en G, definimos la clase lateral izquierda aH = { ah  : h en H }. Como a es invertible, el mapa φ: H → aH dado por φ ( h ) = ah es una biyección . Además, cada elemento de G está contenido precisamente en una clase lateral izquierda de H ; las clases laterales izquierda son las clases de equivalencia correspondientes a la relación de equivalencia un ₁ ~ un ₂ si y sólo si un ₁ ^-1 un ₂ es en H . El número de clases laterales izquierdas de H se denomina índice de H en G y se denota por [ G  : H ].

El teorema de Lagrange establece que para un grupo finito G y un subgrupo H ,

${\ Displaystyle [G: H] = {| G | \ over | H |}}$

donde | G | y | H | denotan los órdenes de G y H , respectivamente. En particular, el orden de cada subgrupo de G (y el orden de cada elemento de G ) debe ser un divisor de | G |.

Las clases laterales derechas se definen de forma análoga: Ha = { ha  : h en H }. También son las clases de equivalencia para una relación de equivalencia adecuada y su número es igual a [ G  : H ].

Si aH = Ha para cada a en G , entonces se dice que H es un subgrupo normal . Cada subgrupo del índice 2 es normal: las clases laterales izquierdas y también las clases laterales derechas son simplemente el subgrupo y su complemento. De manera más general, si p es el número primo más bajo que divide el orden de un grupo finito G, entonces cualquier subgrupo del índice p (si existe) es normal.

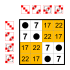
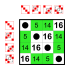
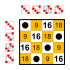
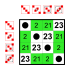
Ejemplo: subgrupos de Z ₈

Sea G el grupo cíclico Z ₈ cuyos elementos son

${\ Displaystyle G = \ left \ {0,4,2,6,1,5,3,7 \ right \}}$

y cuya operación de grupo es suma módulo ocho . Su mesa Cayley es

+	0	4	2	6	1	5	3	7
0	0	4	2	6	1	5	3	7
4	4	0	6	2	5	1	7	3
2	2	6	4	0	3	7	5	1
6	6	2	0	4	7	3	1	5
1	1	5	3	7	2	6	4	0
5	5	1	7	3	6	2	0	4
3	3	7	5	1	4	0	6	2
7	7	3	1	5	0	4	2	6

Este grupo tiene dos subgrupos no triviales: J = {0,4} y H = {0,4,2,6} , donde J es también un subgrupo de H . La tabla Cayley para H es el cuadrante superior izquierdo de la tabla Cayley para G ; La tabla de Cayley para J es el cuadrante superior izquierdo de la tabla de Cayley para H . El grupo G es cíclico , al igual que sus subgrupos. En general, los subgrupos de grupos cíclicos también son cíclicos.

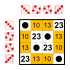
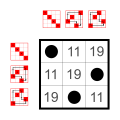
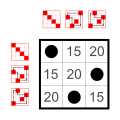
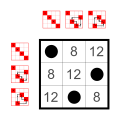
Ejemplo: subgrupos de S ₄ (el grupo simétrico de 4 elementos)

Cada grupo tiene tantos subgrupos pequeños como elementos neutrales en la diagonal principal:

El grupo trivial y los grupos de dos elementos Z ₂ . Estos pequeños subgrupos no se cuentan en la siguiente lista.

El grupo simétrico S 4 que muestra todas las permutaciones de 4 elementos

Los 30 subgrupos Simplificado Diagramas de Hasse de la red de subgrupos de S 4

12 elementos

8 elementos

Grupo diedro de orden 8 Subgrupos:

Grupo diedro de orden 8 Subgrupos:

Grupo diedro de orden 8 Subgrupos:

6 elementos

Grupo simétrico S 3 Subgrupo:

Grupo simétrico S 3 Subgrupo:

Grupo simétrico S 3 Subgrupo:

Grupo simétrico S 3 Subgrupo:

4 elementos

Klein de cuatro grupos

Klein de cuatro grupos

Klein de cuatro grupos

Klein de cuatro grupos

Grupo cíclico Z 4

Grupo cíclico Z 4

Grupo cíclico Z 4

3 elementos

Grupo cíclico Z 3

Grupo cíclico Z 3

Grupo cíclico Z 3

Grupo cíclico Z 3

Otros ejemplos

• Los enteros pares son un subgrupo del grupo aditivo de enteros: cuando suma dos números pares, obtiene un número par.
• Un ideal en un anillo es un subgrupo del grupo aditivo de .${\ Displaystyle R}$${\ Displaystyle R}$
• Un subespacio lineal de un espacio vectorial es un subgrupo del grupo aditivo de vectores.
• Sea un grupo abeliano ; los elementos de que tienen un período finito forman un subgrupo de llamado subgrupo de torsión de .${\ Displaystyle A}$${\ Displaystyle A}$${\ Displaystyle A}$${\ Displaystyle A}$

Ver también

• Subgrupo Cartan
• Subgrupo apropiado
• Subgrupo estable
• Subgrupo de punto fijo
• Prueba de subgrupos

Notas

Referencias

• Jacobson, Nathan (2009), Álgebra básica , 1 (2a ed.), Dover, ISBN 978-0-486-47189-1.
• Hungerford, Thomas (1974), Álgebra (1ª ed.), Springer-Verlag, ISBN 9780387905181.
• Artin, Michael (2011), Álgebra (2.a ed.), Prentice Hall, ISBN 9780132413770.
• Dummit, David S .; Foote, Richard M. (2004). Álgebra abstracta (3ª ed.). Hoboken, Nueva Jersey: Wiley. ISBN 9780471452348. OCLC  248917264 .