Algoritmo rho de Pollard - Pollard's rho algorithm
El algoritmo rho de Pollard es un algoritmo para la factorización de enteros . Fue inventado por John Pollard en 1975. Utiliza solo una pequeña cantidad de espacio y su tiempo de ejecución esperado es proporcional a la raíz cuadrada del tamaño del factor primo más pequeño del número compuesto que se factoriza.
Ideas centrales
El algoritmo se utiliza para factorizar un número , donde es un factor no trivial. Un modulo polinomio , llamado (por ejemplo, ), se utiliza para generar una secuencia pseudoaleatoria : un valor inicial, por ejemplo 2, se elige, y la secuencia continúa como , , , etc. La secuencia está relacionada con otra secuencia . Dado que no se conoce de antemano, esta secuencia no se puede calcular explícitamente en el algoritmo. Sin embargo, en él radica la idea central del algoritmo.
Debido a que el número de valores posibles para estas secuencias es finito, tanto la secuencia, que es mod , como la secuencia se repetirán eventualmente, aunque estos valores sean desconocidos. Si las secuencias se comportaran como números aleatorios, la paradoja del cumpleaños implica que se esperaría que el número de antes de que ocurra una repetición sea , donde es el número de valores posibles. Por lo tanto, es probable que la secuencia se repita mucho antes que la secuencia . Una vez que una secuencia tiene un valor repetido, la secuencia circulará, porque cada valor depende solo del anterior. Esta estructura de eventual ciclismo da lugar al nombre de "rho algoritmo", debido a la similitud con la forma del carácter griego ρ cuando los valores , , etc. se representan como nodos de un grafo dirigido .
Esto es detectado por el algoritmo de búsqueda de ciclo de Floyd : se mantienen dos nodos y (es decir, y ). En cada paso, uno se mueve al siguiente nodo de la secuencia y el otro avanza en dos nodos. Después de eso, se comprueba si . Si no es 1, esto implica que hay una repetición en la secuencia (es decir, esto funciona porque si es igual que , la diferencia entre y es necesariamente un múltiplo de . Aunque esto siempre ocurre eventualmente, el mayor común resultante El divisor (MCD) es un divisor distinto de 1. Este puede ser el mismo, ya que las dos secuencias pueden repetirse al mismo tiempo, en este caso (poco común) el algoritmo falla y puede repetirse con un parámetro diferente.
Algoritmo
El algoritmo toma como entradas n , el número entero a factorizar; y , un polinomio en x calculado módulo n . En el algoritmo original , pero hoy en día es más común usar . La salida es un factor no trivial de n , o falla. Realiza los siguientes pasos:
x ← 2
y ← 2
d ← 1
while d = 1:
x ← g(x)
y ← g(g(y))
d ← gcd(|x - y|, n)
if d = n:
return failure
else:
return d
Aquí x e Y corresponde a y en la sección acerca de la idea central. Tenga en cuenta que este algoritmo puede fallar al encontrar un factor no trivial incluso cuando n es compuesto. En ese caso, el método se puede volver a intentar, utilizando un valor inicial distinto de 2 o diferente .
Ejemplo de factorización
Deja y .
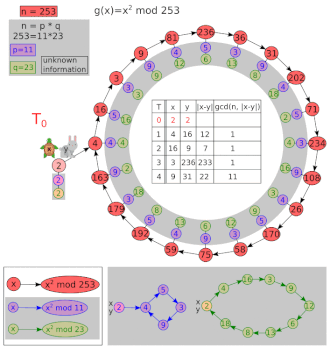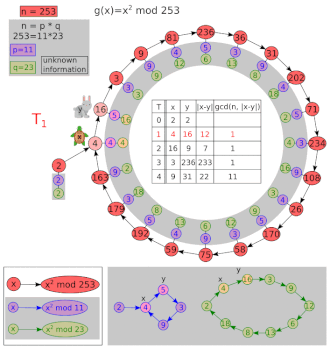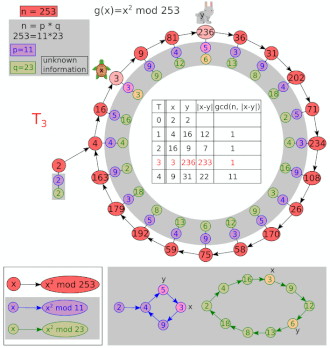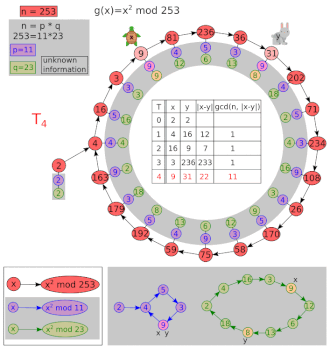
| I | X | y | MCD (| x - y |, 8051) |
|---|---|---|---|
| 1 | 5 | 26 | 1 |
| 2 | 26 | 7474 | 1 |
| 3 | 677 | 871 | 97 |
| 4 | 7474 | 1481 | 1 |
97 es un factor no trivial de 8051. Los valores iniciales distintos de x = y = 2 pueden dar el cofactor (83) en lugar de 97. Una iteración adicional se muestra arriba para aclarar que y se mueve dos veces más rápido que x . Tenga en cuenta que incluso después de una repetición, el GCD puede volver a 1.
Variantes
En 1980, Richard Brent publicó una variante más rápida del algoritmo rho. Usó las mismas ideas centrales que Pollard pero un método diferente de detección de ciclos, reemplazando el algoritmo de búsqueda de ciclos de Floyd con el método de búsqueda de ciclos de Brent relacionado .
Pollard y Brent realizaron una mejora adicional. Observaron que si , entonces también para cualquier número entero positivo . En particular, en lugar de calcular en cada paso, es suficiente definir como el producto de 100 términos consecutivos módulo y luego calcular uno solo . Se produce una aceleración importante ya que los pasos de 100 gcd se reemplazan con un módulo de 99 multiplicaciones y un solo mcd . Ocasionalmente, puede hacer que el algoritmo falle al introducir un factor repetido, por ejemplo, cuando es un cuadrado. Pero luego es suficiente volver al término gcd anterior , donde , y usar el algoritmo ρ regular desde allí.
Solicitud
El algoritmo es muy rápido para números con factores pequeños, pero más lento en los casos en que todos los factores son grandes. El éxito más notable del algoritmo ρ fue la factorización del número de Fermat F 8 = 1238926361552897 × 93461639715357977769163558199606896584051237541638188580280321. El algoritmo ρ fue una buena elección para F 8 porque el factor primo p = 1238926361552897 es mucho más pequeño que el otro factor. La factorización tomó 2 horas en un UNIVAC 1100/42 .
El ejemplo n = 10403 = 101 · 103
En este ejemplo, solo se calcula una secuencia y el mcd se calcula dentro del bucle que detecta el ciclo.
Ejemplo de código C
El siguiente ejemplo de código encuentra el factor 101 de 10403 con un valor inicial de x = 2.
#include <stdio.h>
#include <stdlib.h>
int gcd(int a, int b)
{
int remainder;
while (b != 0) {
remainder = a % b;
a = b;
b = remainder;
}
return a;
}
int main (int argc, char *argv[])
{
int number = 10403, loop = 1, count;
int x_fixed = 2, x = 2, size = 2, factor;
do {
printf("---- loop %4i ----\n", loop);
count = size;
do {
x = (x * x + 1) % number;
factor = gcd(abs(x - x_fixed), number);
printf("count = %4i x = %6i factor = %i\n", size - count + 1, x, factor);
} while (--count && (factor == 1));
size *= 2;
x_fixed = x;
loop = loop + 1;
} while (factor == 1);
printf("factor is %i\n", factor);
return factor == number ? EXIT_FAILURE : EXIT_SUCCESS;
}
El código anterior mostrará el progreso del algoritmo, así como los valores intermedios. La línea de salida final será "el factor es 101". El código solo funcionará para valores de prueba pequeños, ya que se producirá un desbordamiento en los tipos de datos enteros durante el cuadrado de x.
Muestra de código de Python
from itertools import count
from math import gcd
import sys
number, x = 10403, 2
for cycle in count(1):
y = x
for i in range(2 ** cycle):
x = (x * x + 1) % number
factor = gcd(x - y, number)
if factor > 1:
print("factor is", factor)
sys.exit()
Los resultados
En la siguiente tabla, la tercera y cuarta columnas contienen información secreta que no conoce la persona que intenta factorizar pq = 10403. Se incluyen para mostrar cómo funciona el algoritmo. Comenzando con x = 2, el algoritmo produce los siguientes números:
| paso | ||||
|---|---|---|---|---|
| 2 | 2 | 2 | 2 | 0 |
| 5 | 2 | 5 | 2 | 1 |
| 26 | 2 | 26 | 2 | 2 |
| 677 | 26 | 71 | 26 | 3 |
| 598 | 26 | 93 | 26 | 4 |
| 3903 | 26 | sesenta y cinco | 26 | 5 |
| 3418 | 26 | 85 | 26 | 6 |
| 156 | 3418 | 55 | 85 | 7 |
| 3531 | 3418 | 97 | 85 | 8 |
| 5168 | 3418 | 17 | 85 | 9 |
| 3724 | 3418 | 88 | 85 | 10 |
| 978 | 3418 | 69 | 85 | 11 |
| 9812 | 3418 | 15 | 85 | 12 |
| 5983 | 3418 | 24 | 85 | 13 |
| 9970 | 3418 | 72 | 85 | 14 |
| 236 | 9970 | 34 | 72 | 15 |
| 3682 | 9970 | 46 | 72 | dieciséis |
| 2016 | 9970 | 97 | 72 | 17 |
| 7087 | 9970 | 17 | 72 | 18 |
| 10289 | 9970 | 88 | 72 | 19 |
| 2594 | 9970 | 69 | 72 | 20 |
| 8499 | 9970 | 15 | 72 | 21 |
| 4973 | 9970 | 24 | 72 | 22 |
| 2799 | 9970 | 72 | 72 | 23 |
El primer módulo de repetición 101 es 97 que se produce en el paso 17. La repetición no se detecta hasta el paso 23, cuando . Esto hace que sea , y se encuentra un factor.
Complejidad
Si el número pseudoaleatorio que ocurre en el algoritmo ρ de Pollard fuera un número aleatorio real, se seguiría que el éxito se lograría la mitad de las veces, por la paradoja del cumpleaños en iteraciones. Se cree que el mismo análisis se aplica también al algoritmo rho real, pero esta es una afirmación heurística, y el análisis riguroso del algoritmo permanece abierto.
Ver también
Referencias
Otras lecturas
- Katz, Jonathan; Lindell, Yehuda (2007). "Capítulo 8". Introducción a la criptografía moderna . Prensa CRC.
- Samuel S. Wagstaff, Jr. (2013). La alegría de la factorización . Providence, RI: Sociedad Matemática Estadounidense. págs. 135-138. ISBN 978-1-4704-1048-3.












































