Octonion - Octonion

Octonions
Símbolo	${\ Displaystyle \ mathbb {O}}$
Escribe	Álgebra hipercompleja
Unidades	e 0 , ..., e 7
Identidad multiplicativa	e 0
Principales propiedades	No conmutativo No asociativo
Sistemas comunes
Sistemas menos comunes Octonions ( ) Sedenions ( ) ${\ Displaystyle \ mathbb {O}}$${\ Displaystyle \ mathbb {S}}$

En matemáticas , los octoniones son un álgebra de división normalizada sobre los números reales , una especie de sistema numérico hipercomplejo . Los octoniones suelen estar representados por la letra mayúscula O, utilizando negrita O o negrita en negrita . Los octoniones tienen ocho dimensiones ; el doble de dimensiones de los cuaterniones , de los cuales son una extensión. Son no conmutativos y no asociativos , pero satisfacen una forma más débil de asociatividad; es decir, son alternativas . También son asociativos de poder . ${\ Displaystyle \ mathbb {O}}$

Los octoniones no son tan conocidos como los cuaterniones y los números complejos , que son mucho más estudiados y utilizados. Los octoniones están relacionados con estructuras excepcionales en matemáticas, entre ellos los grupos de Lie excepcionales . Los octoniones tienen aplicaciones en campos como la teoría de cuerdas , la relatividad especial y la lógica cuántica . La aplicación de la construcción Cayley-Dickson a los octoniones produce las sedeniones .

Historia

Los octoniones fueron descubiertos en 1843 por John T. Graves , inspirado por el descubrimiento de los cuaterniones por su amigo William Rowan Hamilton . Graves llamó a su descubrimiento "octavas", y las mencionó en una carta a Hamilton fechada el 16 de diciembre de 1843. Publicó por primera vez su resultado un poco más tarde que el artículo de Arthur Cayley . Los octoniones fueron descubiertos de forma independiente por Cayley y, a veces, se denominan "números de Cayley" o "álgebra de Cayley". Hamilton describió la historia temprana del descubrimiento de Graves.

Definición

Los octoniones se pueden considerar como octetos (u 8 tuplas) de números reales. Cada octonión es una combinación lineal real de los octoniones unitarios :

${\ Displaystyle \ {e_ {0}, e_ {1}, e_ {2}, e_ {3}, e_ {4}, e_ {5}, e_ {6}, e_ {7} \},}$

donde e ₀ es el elemento escalar o real; se puede identificar con el número real 1. Es decir, cada octonión x se puede escribir en la forma

${\ Displaystyle x = x_ {0} e_ {0} + x_ {1} e_ {1} + x_ {2} e_ {2} + x_ {3} e_ {3} + x_ {4} e_ {4} + x_ {5} e_ {5} + x_ {6} e_ {6} + x_ {7} e_ {7}, \,}$

con coeficientes reales x _i .

La suma y resta de octoniones se realiza sumando y restando los términos correspondientes y, por tanto, sus coeficientes, como los cuaterniones. La multiplicación es más compleja. La multiplicación es distributiva sobre la suma, por lo que el producto de dos octoniones se puede calcular sumando los productos de todos los términos, nuevamente como cuaterniones. El producto de cada par de términos se puede dar mediante la multiplicación de los coeficientes y una tabla de multiplicar de las octoniones unitarias, como esta (debido a Cayley, 1845, y Graves, 1843):

${\ Displaystyle e_ {i} e_ {j}}$		${\ Displaystyle e_ {j}}$
		${\ Displaystyle e_ {0}}$	${\ Displaystyle e_ {1}}$	${\ Displaystyle e_ {2}}$	${\ Displaystyle e_ {3}}$	${\ Displaystyle e_ {4}}$	${\ Displaystyle e_ {5}}$	${\ Displaystyle e_ {6}}$	${\ Displaystyle e_ {7}}$
${\ Displaystyle e_ {i}}$	${\ Displaystyle e_ {0}}$	${\ Displaystyle e_ {0}}$	${\ Displaystyle e_ {1}}$	${\ Displaystyle e_ {2}}$	${\ Displaystyle e_ {3}}$	${\ Displaystyle e_ {4}}$	${\ Displaystyle e_ {5}}$	${\ Displaystyle e_ {6}}$	${\ Displaystyle e_ {7}}$
	${\ Displaystyle e_ {1}}$	${\ Displaystyle e_ {1}}$	${\ Displaystyle -e_ {0}}$	${\ Displaystyle e_ {3}}$	${\ Displaystyle -e_ {2}}$	${\ Displaystyle e_ {5}}$	${\ Displaystyle -e_ {4}}$	${\ Displaystyle -e_ {7}}$	${\ Displaystyle e_ {6}}$
	${\ Displaystyle e_ {2}}$	${\ Displaystyle e_ {2}}$	${\ Displaystyle -e_ {3}}$	${\ Displaystyle -e_ {0}}$	${\ Displaystyle e_ {1}}$	${\ Displaystyle e_ {6}}$	${\ Displaystyle e_ {7}}$	${\ Displaystyle -e_ {4}}$	${\ Displaystyle -e_ {5}}$
	${\ Displaystyle e_ {3}}$	${\ Displaystyle e_ {3}}$	${\ Displaystyle e_ {2}}$	${\ Displaystyle -e_ {1}}$	${\ Displaystyle -e_ {0}}$	${\ Displaystyle e_ {7}}$	${\ Displaystyle -e_ {6}}$	${\ Displaystyle e_ {5}}$	${\ Displaystyle -e_ {4}}$
	${\ Displaystyle e_ {4}}$	${\ Displaystyle e_ {4}}$	${\ Displaystyle -e_ {5}}$	${\ Displaystyle -e_ {6}}$	${\ Displaystyle -e_ {7}}$	${\ Displaystyle -e_ {0}}$	${\ Displaystyle e_ {1}}$	${\ Displaystyle e_ {2}}$	${\ Displaystyle e_ {3}}$
	${\ Displaystyle e_ {5}}$	${\ Displaystyle e_ {5}}$	${\ Displaystyle e_ {4}}$	${\ Displaystyle -e_ {7}}$	${\ Displaystyle e_ {6}}$	${\ Displaystyle -e_ {1}}$	${\ Displaystyle -e_ {0}}$	${\ Displaystyle -e_ {3}}$	${\ Displaystyle e_ {2}}$
	${\ Displaystyle e_ {6}}$	${\ Displaystyle e_ {6}}$	${\ Displaystyle e_ {7}}$	${\ Displaystyle e_ {4}}$	${\ Displaystyle -e_ {5}}$	${\ Displaystyle -e_ {2}}$	${\ Displaystyle e_ {3}}$	${\ Displaystyle -e_ {0}}$	${\ Displaystyle -e_ {1}}$
	${\ Displaystyle e_ {7}}$	${\ Displaystyle e_ {7}}$	${\ Displaystyle -e_ {6}}$	${\ Displaystyle e_ {5}}$	${\ Displaystyle e_ {4}}$	${\ Displaystyle -e_ {3}}$	${\ Displaystyle -e_ {2}}$	${\ Displaystyle e_ {1}}$	${\ Displaystyle -e_ {0}}$

La mayoría de los elementos fuera de la diagonal de la tabla son antisimétricos, lo que la convierte en una matriz casi simétrica, excepto los elementos de la diagonal principal, así como la fila y la columna para las que e ₀ es un operando.

La tabla se puede resumir de la siguiente manera:

${\ Displaystyle e_ {i} e_ {j} = {\ begin {cases} e_ {j}, & {\ text {if}} i = 0 \\ e_ {i}, & {\ text {if}} j = 0 \\ - \ delta _ {ij} e_ {0} + \ varepsilon _ {ijk} e_ {k}, & {\ text {de otro modo}} \ end {cases}}}$

donde δ _ij es el delta de Kronecker (igual a 1 si y solo si i = j ), y ε _ijk es un tensor completamente antisimétrico con valor 1 cuando ijk = 123, 145, 176, 246, 257, 347, 365 .

Sin embargo, la definición anterior no es única; es sólo una de las 480 posibles definiciones para la multiplicación de octoniones con e ₀ = 1 . Los demás pueden obtenerse permutando y cambiando los signos de los elementos básicos no escalares { e ₁ , e ₂ , e ₃ , e ₄ , e ₅ , e ₆ , e ₇ } . Las 480 álgebras diferentes son isomórficas y rara vez es necesario considerar qué regla de multiplicación en particular se usa.

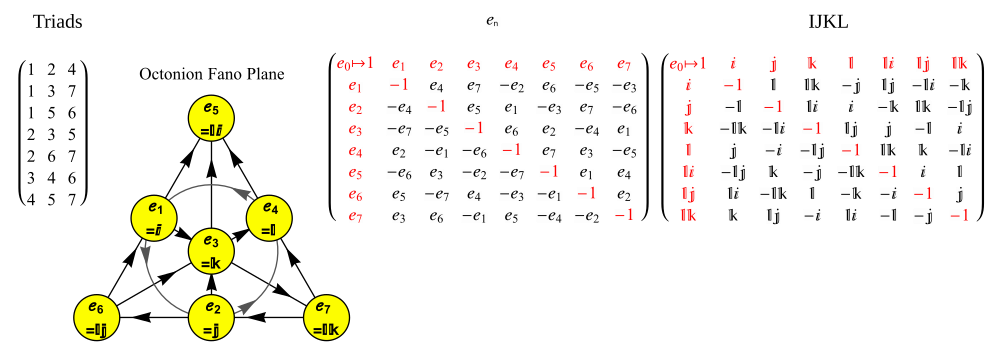
Cada una de estas 480 definiciones es invariante hasta los signos en algún 7 ciclo de los puntos (1234567), y para cada 7 ciclos hay cuatro definiciones, que se diferencian por los signos y la inversión de orden. Una opción común es usar la definición invariante bajo el ciclo de 7 (1234567) con e ₁ e ₂ = e ₄ - usando el diagrama de multiplicación triangular, o el plano de Fano a continuación que también muestra la lista ordenada de 124 tríadas de 7 ciclos basadas y sus matrices de multiplicación asociadas en formato e _n e IJKL.

Una variación de esto que se usa a veces es etiquetar los elementos de la base por los elementos ∞ , 0, 1, 2, ..., 6, de la línea proyectiva sobre el campo finito de orden 7. La multiplicación viene dada por e _∞ = 1 y e ₁ e ₂ = ae ₄ , y todas las expresiones obtenidos de este mediante la adición de una constante ( módulo 7) a todos los subíndices: en otras palabras utilizando las siete triples (124) (235) (346) (450) ( 561) (602) (013). Estas son las palabras de código distintas de cero del código de residuo cuadrático de longitud 7 sobre el campo de Galois de dos elementos, GF (2) . Existe una simetría de orden 7 dada al agregar una constante mod 7 a todos los subíndices, y también una simetría de orden 3 dada al multiplicar todos los subíndices por uno de los residuos cuadráticos 1, 2, 4 mod 7.

La tabla de multiplicar para un álgebra geométrica de firma (−−−−) se puede dar en términos de los siguientes 7 triples cuaterniónicos (omitiendo el elemento de identidad):

( Yo , j , k ), ( yo , J , k ), ( yo , j , K ), ( yo , J , K ), (∗ yo , yo , metro ), (∗ J , j , metro ), (∗ K , k , m )

en el que los elementos en minúscula son vectores y los mayúsculas son bivectores y ∗ = mijk (que es el operador estrella de Hodge ). Si se obliga a ∗ a ser igual a la identidad, la multiplicación deja de ser asociativa, pero ∗ puede eliminarse de la tabla de multiplicar, lo que da como resultado una tabla de multiplicar octoniones.

Al mantener ∗ = mijk asociativo y, por lo tanto, no reducir el álgebra geométrica de 4 dimensiones a un octonión, toda la tabla de multiplicar se puede derivar de la ecuación para ∗ . Considere las matrices gamma . La fórmula que define la quinta matriz gamma muestra que es el ∗ de un álgebra geométrica de cuatro dimensiones de las matrices gamma.

Construcción Cayley – Dickson

Una forma más sistemática de definir los octoniones es mediante la construcción Cayley-Dickson. Así como los cuaterniones se pueden definir como pares de números complejos, los octoniones se pueden definir como pares de cuaterniones. La suma se define por pares. El producto de dos pares de cuaterniones ( a , b ) y ( c , d ) se define por

${\ Displaystyle (a, b) (do, d) = (ac-d ^ {*} b, da + bc ^ {*}),}$

donde z * denota el conjugado del cuaternión z . Esta definición es equivalente a la dada arriba cuando las ocho unidades de octoniones se identifican con los pares

(1, 0), ( i , 0), ( j , 0), ( k , 0), (0, 1), (0, i ), (0, j ), (0, k )

Fano avión mnemónico

Un mnemónico para los productos de las octoniones unitarias.

Una visualización nemotécnica en 3D que muestra las 7 tríadas como hiperplanos a través del vértice real ( e ₀ ) del ejemplo del octonión dado anteriormente.

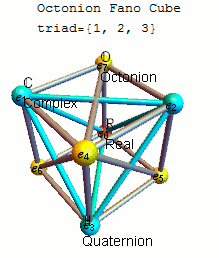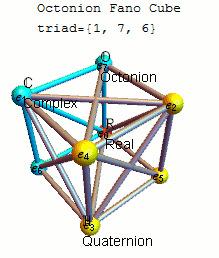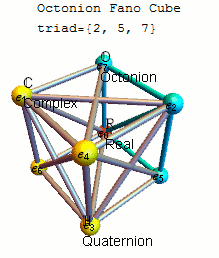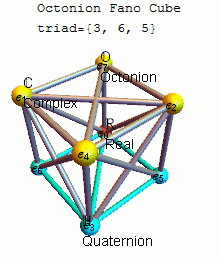
Un mnemónico conveniente para recordar los productos de octoniones unitarios viene dado por el diagrama, que representa la tabla de multiplicar de Cayley y Graves. Este diagrama con siete puntos y siete líneas (el círculo que pasa por 1, 2 y 3 se considera una línea) se llama plano de Fano . Las líneas son direccionales. Los siete puntos corresponden a los siete elementos básicos estándar de Im ( O ) (consulte la definición a continuación ). Cada par de puntos distintos se encuentra en una línea única y cada línea atraviesa exactamente tres puntos.

Sea ( a , b , c ) un triple ordenado de puntos que se encuentran en una línea dada con el orden especificado por la dirección de la flecha. Entonces la multiplicación viene dada por

ab = c y ba = - c

junto con permutaciones cíclicas . Estas reglas junto con

• 1 es la identidad multiplicativa,
• mi²
  _yo= −1 para cada punto del diagrama

define completamente la estructura multiplicativa de los octoniones. Cada una de las líneas de siete genera una subálgebra de O isomorfo a los cuaterniones H .

Conjugado, norma e inverso

El conjugado de un octonion

${\ Displaystyle x = x_ {0} \, e_ {0} + x_ {1} \, e_ {1} + x_ {2} \, e_ {2} + x_ {3} \, e_ {3} + x_ {4} \, e_ {4} + x_ {5} \, e_ {5} + x_ {6} \, e_ {6} + x_ {7} \, e_ {7}}$

es dado por

${\ Displaystyle x ^ {*} = x_ {0} \, e_ {0} -x_ {1} \, e_ {1} -x_ {2} \, e_ {2} -x_ {3} \, e_ { 3} -x_ {4} \, e_ {4} -x_ {5} \, e_ {5} -x_ {6} \, e_ {6} -x_ {7} \, e_ {7}.}$

La conjugación es una involución de O y satisface ( xy ) * = y * x * (observe el cambio en el orden).

La parte real de x viene dada por

${\ Displaystyle {\ frac {x + x ^ {*}} {2}} = x_ {0} \, e_ {0}}$

y la parte imaginaria por

${\ Displaystyle {\ frac {xx ^ {*}} {2}} = x_ {1} \, e_ {1} + x_ {2} \, e_ {2} + x_ {3} \, e_ {3} + x_ {4} \, e_ {4} + x_ {5} \, e_ {5} + x_ {6} \, e_ {6} + x_ {7} \, e_ {7}.}$

El conjunto de todos los octoniones puramente imaginarios abarca un subespacio de 7 dimensiones de O , denotado Im ( O ) .

La conjugación de octoniones satisface la ecuación

${\ Displaystyle x ^ {*} = - {\ tfrac {1} {6}} {\ bigl (} x + (e_ {1} x) e_ {1} + (e_ {2} x) e_ {2} + (e_ {3} x) e_ {3} + (e_ {4} x) e_ {4} + (e_ {5} x) e_ {5} + (e_ {6} x) e_ {6} + (e_ {7} x) e_ {7} {\ bigr)}.}$

El producto de un octonión con su conjugado, x * x = xx * , es siempre un número real no negativo:

${\ Displaystyle x ^ {*} x = x_ {0} ^ {2} + x_ {1} ^ {2} + x_ {2} ^ {2} + x_ {3} ^ {2} + x_ {4} ^ {2} + x_ {5} ^ {2} + x_ {6} ^ {2} + x_ {7} ^ {2}.}$

Usando esto, la norma de un octonión se puede definir, como

${\ Displaystyle \ | x \ | = {\ sqrt {x ^ {*} x}}.}$

Esta norma está de acuerdo con la norma euclidiana estándar de 8 dimensiones en R ⁸ .

La existencia de una norma de O implica la existencia de inversos para cada elemento no nulo de O . La inversa de x ≠ 0 , que es el octonión único x ^{−1 que} satisface xx ⁻¹ = x ⁻¹ x = 1 , está dada por

${\ Displaystyle x ^ {- 1} = {\ frac {x ^ {*}} {\ | x \ | ^ {2}}}.}$

Propiedades

La multiplicación octoniónica no es conmutativa :

e _i e _j = - e _j e _i ≠ e _j e _i si i , j son distintos y distintos de cero,

ni asociativo :

( e _i e _j ) e _k = - e _i ( e _j e _k ) ≠ e _i ( e _j e _k ) si i , j , k son distintos, distintos de cero y e _i e _j ≠ ± e _k .

Los octoniones satisfacen una forma más débil de asociatividad: son alternativos. Esto significa que la subálgebra generada por dos elementos es asociativa. En realidad, se puede demostrar que la subálgebra generada por dos elementos cualesquiera de O es isomorfa a R , C o H , todos los cuales son asociativos. Debido a su falta de asociatividad, octoniones no pueden ser representados por un subálgebra de un anillo de la matriz por encima , a diferencia de los números reales, números complejos y cuaterniones. ${\ Displaystyle \ mathbb {R}}$

Los octoniones retienen una propiedad importante compartida por R , C y H : la norma sobre O satisface

${\ Displaystyle \ | xy \ | = \ | x \ | \ | y \ |.}$

Esta ecuación significa que los octoniones forman un álgebra de composición . Todas las álgebras de dimensiones superiores definidas por la construcción de Cayley-Dickson (comenzando con las sedeniones ) no satisfacen esta propiedad. Todos tienen divisores cero .

Existen sistemas de números más amplios que tienen un módulo multiplicativo (por ejemplo, sedeniones cónicas de 16 dimensiones). Su módulo se define de manera diferente a su norma, y ​​también contienen divisores cero.

Como lo muestra Hurwitz , R , C , H y O son las únicas álgebras de división normalizadas sobre los números reales. Estas cuatro álgebras también forman la única alternativa, álgebras de división de dimensión finita sobre los números reales ( hasta el isomorfismo).

Al no ser asociativos, los elementos distintos de cero de O no forman un grupo . Sin embargo, forman un bucle , específicamente un bucle de Moufang .

Conmutador y producto cruzado

El conmutador de dos octoniones x y y está dada por

${\ Displaystyle [x, y] = xy-yx.}$

Esto es antisimétrico e imaginario. Si se considera solo como un producto en el subespacio imaginario Im ( O ) , define un producto en ese espacio, el producto cruzado de siete dimensiones , dado por

${\ Displaystyle x \ times y = {\ tfrac {1} {2}} (xy-yx).}$

Como el producto cruzado en tres dimensiones, este es un vector ortogonal ax e y con magnitud

${\ Displaystyle \ | x \ times y \ | = \ | x \ | \ | y \ | \ sin \ theta.}$

Pero al igual que el producto octonion, no se define de forma única. En cambio, hay muchos productos cruzados diferentes, cada uno de los cuales depende de la elección del producto octonión.

Automorfismos

Un automorfismo , A , de los octoniones es una transformación lineal invertible de O que satisface

${\ Displaystyle A (xy) = A (x) A (y).}$

El conjunto de todos los automorfismos de O forma un grupo llamado G ₂ . El grupo G ₂ es un grupo de Lie real , compacto y simplemente conectado de dimensión 14. Este grupo es el más pequeño de los grupos de Lie excepcionales y es isomorfo al subgrupo de Spin (7) que conserva cualquier vector particular elegido en su 8-dimensión. Representación real del espinor. El grupo Spin (7) es a su vez un subgrupo del grupo de isotopías que se describen a continuación.

Ver también : PSL (2,7) - el grupo de automorfismo del plano Fano.

Isotopías

Una isotopía de un álgebra es un triple de mapas lineales biyectivos a , b , c tal que si xy = z entonces a ( x ) b ( y ) = c ( z ) . Para a = b = c esto es lo mismo que un automorfismo. El grupo de isotopías de un álgebra es el grupo de todas las isotopías, que contiene el grupo de automorfismos como subgrupo.

El grupo de isotopía de los octoniones es el grupo Spin ₈ ( R ) , con a , b , c actuando como las tres representaciones de 8 dimensiones. El subgrupo de elementos donde c fija la identidad es el subgrupo Spin ₇ ( R ) , y el subgrupo donde a , b , c fijan la identidad es el grupo de automorfismo G ₂ .

Aplicaciones

Los octoniones juegan un papel importante en la clasificación y construcción de otras entidades matemáticas. Por ejemplo, el grupo de Lie excepcional G ₂ es el grupo de automorfismos de los octoniones, y los otros grupos de Lie excepcionales F ₄ , E ₆ , E ₇ y E ₈ pueden entenderse como las isometrías de ciertos planos proyectivos definidos mediante los octoniones. El conjunto de matrices octoniónicas 3 × 3 autoadjuntas , equipadas con un producto matricial simétrizado, define el álgebra de Albert . En matemáticas discretas , los octoniones proporcionan una derivación elemental de la red Leech y, por lo tanto, están estrechamente relacionados con los grupos simples esporádicos .

Las aplicaciones de los octoniones a la física han sido en gran parte conjeturas. Por ejemplo, en la década de 1970, se intentó comprender los quarks mediante un espacio octoniónico de Hilbert . Se sabe que los octoniones, y el hecho de que solo puedan existir cuatro álgebras de división normalizadas, se relaciona con las dimensiones del espacio-tiempo en las que se pueden construir teorías de campos cuánticos supersimétricos . Además, se han hecho intentos para obtener el modelo estándar de la física de las partículas elementales de construcciones octonionic, por ejemplo utilizando el "Dixon álgebra" C ⊗ H ⊗ O .

Los octoniones también han surgido en el estudio de la entropía de los agujeros negros y la ciencia de la información cuántica .

Los octoniones se han utilizado en soluciones al problema de calibración del ojo de la mano en robótica .

Las redes de octoniones profundos proporcionan un medio de expresión eficiente y compacto en aplicaciones de aprendizaje automático.

Octoniones integrales

Hay varias formas naturales de elegir una forma integral de los octoniones. La más simple es simplemente tomar los octoniones cuyas coordenadas son números enteros . Esto da un álgebra no asociativa sobre los números enteros llamados octoniones graveianos. Sin embargo, no es un orden máximo (en el sentido de la teoría del anillo); hay exactamente siete órdenes máximos que lo contienen. Estos siete órdenes máximos son todos equivalentes bajo automorfismos. La frase "octoniones integrales" generalmente se refiere a una elección fija de uno de estos siete órdenes.

Estos órdenes máximos fueron construidos por Kirmse (1925) , Dickson y Bruck de la siguiente manera. Rotule los ocho vectores base por los puntos de la línea proyectiva sobre el campo con siete elementos. En primer lugar, forme los "enteros de Kirmse": estos consisten en octoniones cuyas coordenadas son enteros o medios enteros, y que son medios enteros (es decir, mitades de enteros impares) en uno de los 16 conjuntos error de harvtxt: sin destino: CITEREFKirmse1925 ( ayuda )

∅ (∞124) (∞235) (∞346) (∞450) (∞561) (∞602) (∞013) (∞0123456) (0356) (1460) (2501) (3612) (4023) (5134 ) (6245)

del código de residuo cuadrático extendido de longitud 8 sobre el campo de dos elementos, dado por ∅ , (∞124) y sus imágenes añadiendo una constante módulo 7, y los complementos de estos ocho conjuntos. Luego cambie el infinito y cualquier otra coordenada; esta operación crea una biyección de los enteros de Kirmse en un conjunto diferente, que es un orden máximo. Hay siete formas de hacer esto, dando siete órdenes máximos, que son todos equivalentes bajo permutaciones cíclicas de las siete coordenadas 0123456. (Kirmse afirmó incorrectamente que los enteros Kirmse también forman un orden máximo, por lo que pensó que había ocho órdenes máximos en lugar de siete, pero como Coxeter (1946) señaló que no se cierran bajo la multiplicación; este error ocurre en varios artículos publicados).

Los enteros de Kirmse y los siete órdenes máximos son todos isométricos a la red E ₈ reescalada por un factor de 1 ⁄ √ 2 . En particular, hay 240 elementos de norma 1 mínima distinta de cero en cada uno de estos órdenes, formando un bucle de Moufang de orden 240.

Los octoniones integrales tienen una "división con el resto" propiedad: dada octoniones integrales una y b ≠ 0 , podemos encontrar q y r con un = qb + r , donde el resto R tiene norma menor que el de b .

En las octoniones integrales, todos los ideales de la izquierda y los ideales de la derecha son ideales de dos lados, y los únicos ideales de dos lados son los ideales principales nO donde n es un número entero no negativo.

Los octoniones integrales tienen una versión de factorización en números primos, aunque no es sencillo de afirmar porque los octoniones no son asociativos, por lo que el producto de los octoniones depende del orden en el que se hacen los productos. Los octoniones integrales irreducibles son exactamente los de la norma prima, y ​​cada octonión integral se puede escribir como un producto de octoniones irreducibles. Más precisamente una octonión integral de norma mn se puede escribir como un producto de octoniones integrales de normas m y n .

El grupo de automorfismos de los octoniones integrales es el grupo G ₂ ( F ₂ ) de orden 12,096, que tiene un subgrupo simple de índice 2 isomorfo al grupo unitario ² A ₂ (3 ² ) . El grupo de isotopías de los octoniones integrales es la doble cobertura perfecta del grupo de rotaciones de la red E ₈ .

Ver también

Notas

Referencias

enlaces externos

• "Números de Cayley" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Wilson, RA (2008), Octonions (PDF) , Notas del seminario de matemáticas puras