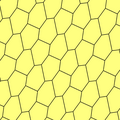
Azulejos hexagonales - Hexagonal tiling
| Azulejos hexagonales | |
|---|---|
 |
|
| Escribe | Azulejos regulares |
| Configuración de vértice | 6.6.6 (o 6 3 ) |
| Configuración de la cara | V3.3.3.3.3.3 (o V3 6 ) |
| Símbolo (s) de Schläfli | {6,3} t {3,6} |
| Símbolo (s) de Wythoff | 3 | 6 2 2 6 | 3 3 3 3 | |
| Diagrama (s) de Coxeter |
|
| Simetría | p6m , [6,3], (* 632) |
| Simetría de rotación | p6 , [6,3] + , (632) |
| Doble | Azulejos triangulares |
| Propiedades | Vértice-transitivo , borde-transitivo , cara-transitivo |
En geometría , el mosaico hexagonal o mosaico hexagonal es un mosaico regular del plano euclidiano , en el que exactamente tres hexágonos se encuentran en cada vértice. Tiene el símbolo de Schläfli de {6,3} o t {3,6} (como un mosaico triangular truncado).
El matemático inglés John Conway lo llamó hextille .
El ángulo interno del hexágono es de 120 grados, por lo que tres hexágonos en un punto forman un total de 360 grados. Es uno de los tres mosaicos regulares del avión . Los otros dos son el mosaico triangular y el mosaico cuadrado .
Aplicaciones
El mosaico hexagonal es la forma más densa de organizar círculos en dos dimensiones. La conjetura del panal establece que el mosaico hexagonal es la mejor manera de dividir una superficie en regiones de igual área con el menor perímetro total. Lord Kelvin investigó la estructura tridimensional óptima para hacer un panal (o más bien, pompas de jabón) , quien creía que la estructura de Kelvin (o celosía cúbica centrada en el cuerpo ) es óptima. Sin embargo, la estructura menos regular de Weaire-Phelan es un poco mejor.
Esta estructura existe de forma natural en forma de grafito , donde cada hoja de grafeno se asemeja a una malla de gallinero, con fuertes enlaces de carbono covalentes. Se han sintetizado láminas tubulares de grafeno; estos se conocen como nanotubos de carbono . Tienen muchas aplicaciones potenciales, debido a su alta resistencia a la tracción y propiedades eléctricas. Silicene es similar.
El alambre de gallinero consiste en una celosía hexagonal (a menudo no regular) de alambres.
El empaque circular más denso está dispuesto como los hexágonos en este mosaico.
Cercado de alambre de gallinero
Un nanotubo de carbono puede verse como un mosaico hexagonal en una superficie cilíndrica
El mosaico hexagonal aparece en muchos cristales. En tres dimensiones, el empaque cerrado cúbico y hexagonal centrado en las caras son estructuras de cristal comunes. Son las empaquetaduras de esferas más densas en tres dimensiones. Estructuralmente, comprenden capas paralelas de mosaicos hexagonales, similar a la estructura del grafito. Se diferencian en la forma en que las capas están escalonadas entre sí, siendo la cúbica centrada en la cara la más regular de las dos. El cobre puro , entre otros materiales, forma una celosía cúbica centrada en las caras.
Colorantes uniformes
Hay tres colores uniformes distintos de un mosaico hexagonal, todos generados a partir de la simetría reflectante de las construcciones de Wythoff . Las ( h , k ) representan la repetición periódica de un mosaico de color, contando las distancias hexagonales como h primero y k segundo. El mismo conteo se usa en los poliedros de Goldberg , con una notación { p +, 3} h , k , y se puede aplicar a teselaciones hiperbólicas para p > 6.
| k-uniforme | 1-uniforme | 2-uniforme | 3-uniforme | ||||
|---|---|---|---|---|---|---|---|
| Simetría | p6m, (* 632) | p3m1, (* 333) | p6m, (* 632) | p6, (632) | |||
| Fotografía |

|

|

|

|

|

|

|
| Colores | 1 | 2 | 3 | 2 | 4 | 2 | 7 |
| (h, k) | (1,0) | (1,1) | (2,0) | (2,1) | |||
| Schläfli | {6,3} | t {3,6} | t {3 [3] } | ||||
| Wythoff | 3 | 6 2 | 2 6 | 3 | 3 3 3 | | ||||
| Coxeter |
|
|
|
||||
| Conway | H | tΔ | cH = t6daH | wH = t6dsH | |||
El mosaico de 3 colores es una teselación generada por los permutoedros de orden 3 .
Baldosas hexagonales biseladas
Una baldosa hexagonal achaflanada que sustituye los cantos por nuevos hexágonos y se transforma en otra baldosa hexagonal. En el límite, las caras originales desaparecen y los nuevos hexágonos degeneran en rombos y se convierte en un mosaico rómbico .

| Hexágonos (H) | Hexágonos biselados (cH) | Rombos (daH) | ||
|---|---|---|---|---|

|

|

|

|

|
Azulejos relacionados
Los hexágonos se pueden diseccionar en conjuntos de 6 triángulos. Este proceso conduce a dos mosaicos uniformes y al mosaico triangular :
| Azulejos regulares | Disección | 2-mosaicos uniformes | Azulejos regulares | |
|---|---|---|---|---|
 Original |
 
|
 1/3 disecado |
 2/3 disecados |
 completamente diseccionado |
| Azulejos regulares | Recuadro | 2-uniformes dobles | Azulejos regulares | |
 Original |

|
 1/3 inserción |
 2/3 inserto |
 completamente insertado |
El mosaico hexagonal se puede considerar un mosaico rómbico alargado , donde cada vértice del mosaico rómbico se estira en un nuevo borde. Esto es similar a la relación del dodecaedro rómbico y las teselaciones del dodecaedro rombo-hexagonal en 3 dimensiones.
 Azulejos rómbicos |
 Azulejos hexagonales |
 La esgrima usa esta relación |
También es posible subdividir los prototipos de ciertos mosaicos hexagonales en dos, tres, cuatro o nueve pentágonos iguales:
 Azulejos pentagonales tipo 1 con superposiciones de hexágonos regulares (cada uno con 2 pentágonos). |
 baldosas pentagonales tipo 3 con superposiciones de hexágonos regulares (cada uno con 3 pentágonos). |
 Azulejo pentagonal tipo 4 con superposiciones de hexágonos semirregulares (cada uno de ellos con 4 pentágonos). |
 Azulejo pentagonal tipo 3 con superposiciones de dos tamaños de hexágonos regulares (compuestos por 3 y 9 pentágonos respectivamente). |
Mutaciones de simetría
Este mosaico está relacionado topológicamente como parte de una secuencia de mosaicos regulares con caras hexagonales , comenzando con el mosaico hexagonal, con el símbolo de Schläfli {6, n} y el diagrama de Coxeter. ![]()
![]()
![]()
![]()
![]() , progresando hasta el infinito.
, progresando hasta el infinito.
| * n 62 mutación de simetría de teselaciones regulares: {6, n } | ||||||||
|---|---|---|---|---|---|---|---|---|
| Esférico | Euclidiana | Azulejos hiperbólicos | ||||||
 {6,2} |
 {6,3} |
 {6,4} |
 {6,5} |
 {6,6} |
 {6,7} |
 {6,8} |
... |
 {6, ∞} |
Este mosaico está relacionado topológicamente con poliedros regulares con figura de vértice n 3 , como parte de la secuencia que continúa en el plano hiperbólico .
| * n 32 mutación de simetría de teselaciones regulares: { n , 3} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Esférico | Euclidiana | Hyperb compacto. | Paraco. | Hiperbólico no compacto | |||||||

|

|

|

|

|

|

|

|

|

|

|

|
| {2,3} | {3,3} | {4,3} | {5,3} | {6,3} | {7,3} | {8,3} | {∞, 3} | {12i, 3} | {9i, 3} | {6i, 3} | {3i, 3} |
Se relaciona de manera similar con los poliedros truncados uniformes con figura de vértice n .6.6.
| * n 32 mutación de simetría de teselaciones truncadas: n .6.6 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sym. * n 42 [n, 3] |
Esférico | Euclides. | Compacto | Parac. | Hiperbólico no compacto | |||||||
| * 232 [2,3] |
* 332 [3,3] |
* 432 [4,3] |
* 532 [5,3] |
* 632 [6,3] |
* 732 [7,3] |
* 832 [8,3] ... |
* ∞32 [∞, 3] |
[12i, 3] | [9i, 3] | [6i, 3] | ||
Figuras truncadas |

|

|

|

|

|

|

|

|

|

|

|
|
| Config. | 2.6.6 | 3.6.6 | 4.6.6 | 5.6.6 | 6.6.6 | 7.6.6 | 8.6.6 | ∞.6.6 | 12i.6.6 | 9i.6.6 | 6i.6.6 | |
figuras n-kis |

|
|

|

|

|

|

|

|
||||
| Config. | V2.6.6 | V3.6.6 | V4.6.6 | V5.6.6 | V6.6.6 | V7.6.6 | V8.6.6 | V∞.6.6 | V12i.6.6 | V9i.6.6 | V6i.6.6 | |
Este mosaico es también parte de una secuencia de poliedros rómbicos truncados y mosaicos con simetría de grupo Coxeter [n, 3] . El cubo puede verse como un hexaedro rómbico donde los rombos son cuadrados. Las formas truncadas tienen n-gones regulares en los vértices truncados y caras hexagonales no regulares.
| Mutaciones de simetría de teselaciones cuasirregulares duales: V (3.n) 2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| * n32 | Esférico | Euclidiana | Hiperbólico | ||||||||
| * 332 | * 432 | * 532 | * 632 | * 732 | * 832 ... | * ∞32 | |||||
| Embaldosado |

|

|

|

|

|

|

|
||||
| Conf. | V (3,3) 2 | V (3,4) 2 | V (3,5) 2 | V (3,6) 2 | V (3,7) 2 | V (3,8) 2 | V (3.∞) 2 | ||||
Construcciones Wythoff a partir de mosaicos hexagonales y triangulares.
Al igual que los poliedros uniformes, hay ocho mosaicos uniformes que pueden basarse en el mosaico hexagonal regular (o el mosaico triangular dual ).
Al dibujar los mosaicos de color rojo en las caras originales, amarillo en los vértices originales y azul a lo largo de los bordes originales, hay 8 formas, 7 que son topológicamente distintas. (El mosaico triangular truncado es topológicamente idéntico al mosaico hexagonal).
| Azulejos uniformes hexagonales / triangulares | ||||||||
|---|---|---|---|---|---|---|---|---|
Dominios fundamentales |
Simetría : [6,3], (* 632) | [6,3] + , (632) | ||||||
| {6,3} | t {6,3} | r {6,3} | t {3,6} | {3,6} | rr {6,3} | tr {6,3} | sr {6,3} | |
|
|
|
|
|
|
|
|
|
|

|

|

|

|

|

|

|

|

|
| Config. | 6 3 | 3.12.12 | (6,3) 2 | 6.6.6 | 3 6 | 3.4.6.4 | 4.6.12 | 3.3.3.3.6 |
Azulejos hexagonales convexos monoédricos
Hay 3 tipos de mosaicos hexagonales convexos monoédricos. Todos son isoédricos . Cada uno tiene variaciones paramétricas dentro de una simetría fija. El tipo 2 contiene reflejos de deslizamiento y es 2-isoédrico que mantiene distintos pares quirales.
Azulejos topológicamente equivalentes
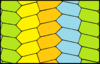
Los mosaicos hexagonales se pueden hacer con la topología {6,3} idéntica a la del mosaico regular (3 hexágonos alrededor de cada vértice). Con caras isoédricas, hay 13 variaciones. La simetría dada asume que todas las caras son del mismo color. Los colores aquí representan las posiciones de la celosía. Las celosías de un solo color (1 teja) son hexágonos paralelos .
| pg (× ×) | p2 (2222) | p3 (333) | pmg (22 *) | |||
|---|---|---|---|---|---|---|

|

|

|

|

|

|
|
| pgg (22 ×) | p31m (3 * 3) | p2 (2222) | cmm (2 * 22) | p6m (* 632) | ||
|

|

|

|

|

|

|
Otros mosaicos hexagonales topológicos con mosaicos isoédricos se ven como cuadriláteros y pentágonos que no son de borde a borde, sino que se interpretan como bordes colineales adyacentes:
| pmg (22 *) | pgg (22 ×) | cmm (2 * 22) | p2 (2222) | |||
|---|---|---|---|---|---|---|
 Paralelogramo |
 Trapezoide |
 Paralelogramo |
 Rectángulo |
 Paralelogramo |
 Rectángulo |
 Rectángulo |
| p2 (2222) | pgg (22 ×) | p3 (333) |
|---|---|---|

|

|

|
Las teselaciones 2 uniformes y 3 uniformes tienen un grado de libertad de rotación que distorsiona 2/3 de los hexágonos, incluido un caso colineal que también puede verse como un mosaico sin borde a borde de hexágonos y triángulos más grandes.
También se puede distorsionar en un patrón tejido tridireccional quiral de 4 colores, distorsionando algunos hexágonos en paralelogramos . El patrón tejido con 2 caras coloreadas tiene simetría rotacional 632 (p6) . Un patrón de chevron tiene simetría pmg (22 *), que se reduce a p1 (°) con 3 o 4 mosaicos de colores.
| Regular | Girado | Regular | Tejido | Cheurón |
|---|---|---|---|---|
| p6m, (* 632) | p6, (632) | p6m (* 632) | p6 (632) | p1 (°) |

|

|

|

|

|
| p3m1, (* 333) | p3, (333) | p6m (* 632) | p2 (2222) | p1 (°) |

|

|

|

|

|
Embalaje circular
El mosaico hexagonal se puede utilizar como un empaque circular , colocando círculos de igual diámetro en el centro de cada punto. Cada círculo está en contacto con otros 3 círculos en el embalaje ( número de besos ). El espacio dentro de cada hexágono permite un círculo, creando el empaque más denso del mosaico triangular , con cada círculo en contacto con un máximo de 6 círculos.
Apeirogons complejos regulares relacionados
Hay 2 apeirogons complejos regulares , que comparten los vértices del mosaico hexagonal. Los apeirogones complejos regulares tienen vértices y aristas, donde las aristas pueden contener 2 o más vértices. Los ápiros regulares p { q } r están restringidos por: 1 / p + 2 / q + 1 / r = 1. Los bordes tienen p vértices y las figuras de los vértices son r -gonales.
El primero está formado por 2 aristas, tres alrededor de cada vértice, el segundo tiene aristas hexagonales, tres alrededor de cada vértice. Un tercer apeirogon complejo, que comparte los mismos vértices, es cuasirregular, que alterna 2 aristas y 6 aristas.

|

|

|
| 2 {12} 3 o |
6 {4} 3 o |
|
|---|
Ver también
- Celosía hexagonal
- Nido de abeja prismático hexagonal
- Mosaicos de polígonos regulares
- Lista de mosaicos uniformes
- Lista de politopos regulares
- Nido de abeja de baldosas hexagonales
- Diseño de juego de mesa de mapa hexagonal
Referencias
- Coxeter, HSM Regular Polytopes , (3a edición, 1973), edición Dover, ISBN 0-486-61480-8 p. 296, Tabla II: Panales regulares
- Grünbaum, Branko ; Shephard, GC (1987). Azulejos y Patrones . Nueva York: WH Freeman. ISBN 0-7167-1193-1.(Capítulo 2.1: Mosaicos regulares y uniformes , págs. 58–65)
- Williams, Robert (1979). La base geométrica de la estructura natural: un libro fuente de diseño . Publicaciones de Dover, Inc. p. 35. ISBN 0-486-23729-X.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss , Las simetrías de las cosas 2008, ISBN 978-1-56881-220-5 [1]
enlaces externos
- ADN | urlname = HexagonalGrid | title = Cuadrícula hexagonal}}
- Klitzing, Richard. "Azulejos euclidianos 2D o3o6x - hexat - O3" .
| Espacio | Familia | / / | ||||
|---|---|---|---|---|---|---|
| E 2 | Azulejos uniformes | {3 [3] } | δ 3 | hδ 3 | qδ 3 | Hexagonal |
| E 3 | Nido de abeja convexo uniforme | {3 [4] } | δ 4 | hδ 4 | qδ 4 | |
| E 4 | Uniforme de 4 panales | {3 [5] } | δ 5 | hδ 5 | qδ 5 | Panal de 24 celdas |
| E 5 | Uniforme de 5 panales | {3 [6] } | δ 6 | hδ 6 | qδ 6 | |
| E 6 | Uniforme de 6 panales | {3 [7] } | δ 7 | hδ 7 | qδ 7 | 2 22 |
| E 7 | Uniforme de 7 panales | {3 [8] } | δ 8 | hδ 8 | qδ 8 | 1 33 • 3 31 |
| E 8 | Uniforme de 8 panal | {3 [9] } | δ 9 | hδ 9 | qδ 9 | 1 52 • 2 51 • 5 21 |
| E 9 | Uniforme de 9 panales | {3 [10] } | δ 10 | hδ 10 | qδ 10 | |
| E 10 | Uniforme de 10 panal | {3 [11] } | δ 11 | hδ 11 | qδ 11 | |
| E n -1 | Uniforme ( n -1) - panal | {3 [n] } | δ n | hδ n | qδ n | 1 k2 • 2 k1 • k 21 |