Teoría del juego y la información - Gambling and information theory

La inferencia estadística podría considerarse como una teoría del juego aplicada al mundo que nos rodea. La miríada de aplicaciones para las medidas de información logarítmica nos dice precisamente cómo hacer la mejor conjetura frente a información parcial. En ese sentido, la teoría de la información podría considerarse una expresión formal de la teoría del juego. No es de extrañar, por tanto, que la teoría de la información tenga aplicaciones en los juegos de azar.

Apuestas Kelly

Las apuestas de Kelly o apuestas proporcionales son una aplicación de la teoría de la información a la inversión y los juegos de azar . Su descubridor fue John Larry Kelly, Jr .

Parte de la idea de Kelly era que el jugador maximizara la expectativa del logaritmo de su capital, en lugar de la ganancia esperada de cada apuesta. Esto es importante, ya que en el último caso, uno se vería obligado a apostar todo lo que tenía cuando se le presentara una apuesta favorable, y si perdiera, no tendría capital para realizar apuestas posteriores. Kelly se dio cuenta de que era el logaritmo del capital del jugador lo que es aditivo en las apuestas secuenciales y "al que se aplica la ley de los grandes números".

Información complementaria

Un poco es la cantidad de entropía en un evento apostado con dos posibles resultados e incluso probabilidades. Obviamente, podríamos duplicar nuestro dinero si supiéramos con certeza de antemano cuál sería el resultado de ese evento. La idea de Kelly fue que no importa cuán complicado sea el escenario de apuestas, podemos usar una estrategia de apuestas óptima, llamada criterio de Kelly , para hacer que nuestro dinero crezca exponencialmente con cualquier información adicional que podamos obtener. El valor de esta información secundaria "ilícita" se mide como información mutua relativa al resultado del evento probable:

${\ Displaystyle {\ begin {alineado} I (X; Y) & = \ mathbb {E} _ {Y} \ {D _ {\ mathrm {KL}} {\ big (} P (X | Y) \ | P (X | I) {\ big)} \} \\ & = \ mathbb {E} _ {Y} \ {D _ {\ mathrm {KL}} {\ big (} P (X | {\ textrm {side} } \ {\ textrm {información}} \ Y) \ | P (X | {\ textrm {declarado}} \ {\ textrm {probabilidades}} \ I) {\ big)} \}, \ end {alineado}} }$

donde Y es la información secundaria, X es el resultado del evento apostable e I es el estado del conocimiento del corredor de apuestas. Este es el promedio de la divergencia de Kullback-Leibler , o ganancia de información, de la a posteriori distribución de probabilidad de X dado el valor de Y con relación a la a priori distribución, o probabilidades indicadas, en X . Tenga en cuenta que la expectativa es asumida Y en vez de X : necesitamos evaluar cómo es exacto, en el largo plazo, nuestra información lateral Y es antes de empezar a apostar dinero real en X . Esta es una aplicación sencilla de la inferencia bayesiana . Tenga en cuenta que la información complementaria Y podría afectar no solo nuestro conocimiento del evento X, sino también el evento en sí. Por ejemplo, Y podría ser un caballo que tenía demasiada avena o no tenía suficiente agua. Las mismas matemáticas se aplican en este caso, porque desde el punto de vista del corredor de apuestas, el arreglo de carrera ocasional ya se tiene en cuenta cuando hace sus probabilidades.

La naturaleza de la información secundaria es extremadamente delicada. Ya hemos visto que puede afectar el evento real, así como nuestro conocimiento del resultado. Supongamos que tenemos un informante, que nos dice que cierto caballo va a ganar. Ciertamente, no queremos apostar todo nuestro dinero en ese caballo solo por un rumor: ese informante puede estar apostando a otro caballo y puede estar difundiendo rumores solo para que él mismo pueda obtener mejores probabilidades. En cambio, como hemos indicado, necesitamos evaluar nuestra información secundaria a largo plazo para ver cómo se correlaciona con los resultados de las carreras. De esta manera podemos determinar exactamente qué tan confiable es nuestro informante, y hacer nuestras apuestas con precisión para maximizar el logaritmo esperado de nuestro capital según el criterio de Kelly. Incluso si nuestro informante nos está mintiendo, podemos sacar provecho de sus mentiras si podemos encontrar alguna correlación inversa entre sus consejos y los resultados reales de la carrera.

Tasa de duplicación

La tasa de duplicación en el juego en una carrera de caballos es

${\ Displaystyle W (b, p) = \ mathbb {E} [\ log _ {2} S (X)] = \ sum _ {i = 1} ^ {m} p_ {i} \ log _ {2} b_ {i} o_ {i}}$

donde hay caballos, la probabilidad de que gane el caballo , la proporción de la riqueza apostada en el caballo y las probabilidades (pago) (por ejemplo, si el caballo que gana paga el doble de la cantidad apostada). Esta cantidad se maximiza mediante el juego proporcional (Kelly): ${\ Displaystyle m}$${\ Displaystyle i}$${\ Displaystyle p_ {i}}$${\ Displaystyle b_ {i}}$${\ Displaystyle o_ {i}}$${\ Displaystyle o_ {i} = 2}$${\ Displaystyle i}$

${\ Displaystyle b = p \,}$

para cual

${\ Displaystyle \ max _ {b} W (b, p) = \ sum _ {i} p_ {i} \ log _ {2} o_ {i} -H (p) \,}$

donde está la entropía de la información . ${\ Displaystyle H (p)}$

Ganancias esperadas

Existe una relación importante pero simple entre la cantidad de información secundaria que obtiene un jugador y el crecimiento exponencial esperado de su capital (Kelly):

${\ Displaystyle \ mathbb {E} \ log K_ {t} = \ log K_ {0} + \ sum _ {i = 1} ^ {t} H_ {i}}$

para una estrategia de apuestas óptima, donde es la capital inicial, es la capital después de la t º apuesta, y es la cantidad de información lateral obtenida relativa a la i º apuesta (en particular, la información mutua en relación con el resultado de cada evento betable) . Esta ecuación se aplica en ausencia de costos de transacción o apuestas mínimas. Cuando se aplican estas restricciones (como sucede invariablemente en la vida real), entra en juego otro concepto importante de juego: el jugador (o inversor sin escrúpulos) debe enfrentar una cierta probabilidad de ruina final, que se conoce como escenario de ruina del jugador . Tenga en cuenta que incluso la comida, la ropa y la vivienda pueden considerarse costos de transacción fijos y, por lo tanto, contribuyen a la probabilidad de ruina final del jugador. ${\ Displaystyle K_ {0}}$${\ Displaystyle K_ {t}}$${\ Displaystyle H_ {i}}$

Esta ecuación fue la primera aplicación de la teoría de la información de Shannon fuera de su paradigma predominante de comunicaciones de datos (Pierce).

Aplicaciones de autoinformación

Sorpresa y evidencia en bits, como medidas logarítmicas de probabilidad y probabilidad respectivamente.

La medida de probabilidad logarítmica de autoinformación o sorpresa, cuyo promedio es entropía / incertidumbre de la información y cuya diferencia promedio es KL-divergencia , tiene aplicaciones al análisis de probabilidades por sí misma. Sus dos fortalezas principales son las sorpresas: (i) reducen las probabilidades minúsculas a números de tamaño manejable, y (ii) suman cada vez que las probabilidades se multiplican.

Por ejemplo, se podría decir que "el número de estados es igual a dos al número de bits", es decir, # estados = 2 ^{# bits} . Aquí, la cantidad que se mide en bits es la medida de información logarítmica mencionada anteriormente. Por lo tanto, hay N bits de sorpresa en colocar todas las caras en el primer lanzamiento de N monedas.

La naturaleza aditiva de las sorpresas y la capacidad de uno para sentir su significado con un puñado de monedas pueden ayudar a poner en contexto eventos improbables (como ganar la lotería o tener un accidente). Por ejemplo, si uno de los 17 millones de boletos es un ganador, entonces la sorpresa de ganar de una sola selección aleatoria es de aproximadamente 24 bits. Lanzar 24 monedas varias veces puede darle una idea de la sorpresa de obtener todas las caras en el primer intento.

La naturaleza aditiva de esta medida también es útil al sopesar alternativas. Por ejemplo, imagine que la sorpresa del daño de una vacuna es de 20 bits. Si la sorpresa de contraer una enfermedad sin ella es de 16 bits, pero la sorpresa de daño por la enfermedad si la contrae es de 2 bits, entonces la sorpresa de daño por NO recibir la vacuna es solo 16 + 2 = 18 bits. Ya sea que decida vacunarse o no (por ejemplo, el costo monetario de pagarla no se incluye en esta discusión), de esa manera al menos puede asumir la responsabilidad de una decisión informada al hecho de que no recibir la vacuna implica más de un poco de riesgo adicional.

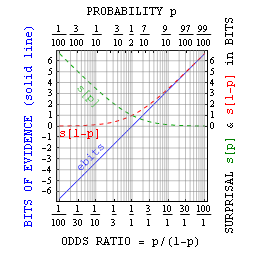
De manera más general, se puede relacionar la probabilidad p con bits de sbits sorprendentes como probabilidad = 1/2 ^sbits . Como se sugirió anteriormente, esto es principalmente útil con pequeñas probabilidades. Sin embargo, Jaynes señaló que con afirmaciones verdadero o falso uno puede también definir los bits de evidencia Ebits como el surprisal contra menos el surprisal para. Esta evidencia en bits se relaciona simplemente con la razón de probabilidades = p / (1-p) = 2 ^ebits , y tiene ventajas similares a las de la propia información.

Aplicaciones en juegos de azar

Se puede pensar en la teoría de la información como una forma de cuantificar la información para tomar la mejor decisión ante una información imperfecta. Es decir, cómo tomar la mejor decisión utilizando solo la información que tiene disponible. El objetivo de apostar es evaluar racionalmente todas las variables relevantes de un juego / carrera / partido incierto, luego compararlas con las evaluaciones de la casa de apuestas, que generalmente se presenta en forma de probabilidades o diferenciales y realizar la apuesta adecuada si las evaluaciones difieren lo suficiente. El área de los juegos de azar donde esto tiene más uso son las apuestas deportivas. El handicap deportivo se presta muy bien a la teoría de la información debido a la disponibilidad de estadísticas. Durante muchos años, destacados economistas han probado diferentes teorías matemáticas utilizando el deporte como laboratorio, con resultados muy diferentes.

Una teoría con respecto a las apuestas deportivas es que se trata de un paseo aleatorio . El paseo aleatorio es un escenario donde la nueva información, precios y retornos fluctuarán por casualidad, esto es parte de la hipótesis del mercado eficiente. La creencia subyacente de la hipótesis del mercado eficiente es que el mercado siempre hará ajustes para cualquier información nueva. Por lo tanto, nadie puede ganarle al mercado porque está operando con la misma información a partir de la cual el mercado se ajustó. Sin embargo, según Fama, para tener un mercado eficiente se deben cumplir tres cualidades:

• No hay costos de transacción en la negociación de valores.
• Toda la información disponible está disponible sin costo para todos los participantes del mercado.
• Todos coinciden en las implicaciones de la información actual para el precio actual y las distribuciones de los precios futuros de cada valor.

Los estadísticos han demostrado que es la tercera condición que permite que la teoría de la información sea útil en el handicap deportivo. Cuando todos no están de acuerdo sobre cómo la información afectará el resultado del evento, recibimos opiniones diferentes.

Ver también

• Principio de indiferencia
• Predicciones de fútbol de la asociación estadística
• Estadísticas avanzadas de la NFL

Referencias

enlaces externos

• Análisis estadístico en modelos deportivos de handicap
• DVOA como variable explicativa