Cascada fraccionada - Fractional cascading

En informática , la cascada fraccionada es una técnica para acelerar una secuencia de búsquedas binarias para el mismo valor en una secuencia de estructuras de datos relacionadas. La primera búsqueda binaria en la secuencia toma una cantidad de tiempo logarítmica, como es estándar para las búsquedas binarias, pero las búsquedas sucesivas en la secuencia son más rápidas. La versión original de cascada fraccionada, presentada en dos artículos por Chazelle y Guibas en 1986 ( Chazelle y Guibas 1986a ; Chazelle y Guibas 1986b ), combinó la idea de cascada, originada en estructuras de datos de búsqueda de rango de Lueker (1978) y Willard (1978). ) , con la idea de muestreo fraccionado, que se originó en Chazelle (1983) . Los autores posteriores introdujeron formas más complejas de cascada fraccionada que permiten que la estructura de los datos se mantenga a medida que los datos cambian mediante una secuencia de eventos discretos de inserción y eliminación.

Ejemplo

Como un ejemplo simple de cascada fraccional, considere el siguiente problema. Se nos da como entrada una colección de k listas ordenadas L _i de números, de manera que la longitud total Σ | L _i | de todas las listas es n , y debemos procesarlas para que podamos realizar búsquedas binarias para un valor de consulta q en cada una de las k listas. Por ejemplo, con k = 4 y n = 17,

L ₁ = 24, 64, 65, 80, 93

L ₂ = 23, 25, 26

L ₃ = 13, 44, 62, 66

L ₄ = 11, 35, 46, 79, 81

La solución más sencilla a este problema de búsqueda es almacenar cada lista por separado. Si lo hacemos, el requisito de espacio es O ( n ), pero el tiempo para realizar una consulta es O ( k log ( n / k )), ya que debemos realizar una búsqueda binaria separada en cada una de las k listas. El peor caso para consultar esta estructura ocurre cuando cada una de las k listas tiene el mismo tamaño n / k , por lo que cada una de las k búsquedas binarias involucradas en una consulta lleva tiempo O (log ( n / k )).

Una segunda solución permite consultas más rápidas a expensas de más espacio: podemos fusionar todas las k listas en una única lista grande L , y asociar con cada elemento x de L una lista de los resultados de la búsqueda de x en cada una de las listas más pequeñas. L _i . Si describimos un elemento de esta lista combinada como x [ un , b , c , d ] donde x es el valor numérico y un , b , c , y d son las posiciones (el primer número tiene la posición 0) del siguiente elemento al menos tan grande como x en cada una de las listas de entrada originales (o la posición después del final de la lista si no existe tal elemento), entonces tendríamos

L = 11 [0,0,0,0], 13 [0,0,0,1], 23 [0,0,1,1], 24 [0,1,1,1], 25 [1, 1,1,1], 26 [1,2,1,1],

35 [1,3,1,1], 44 [1,3,1,2], 46 [1,3,2,2], 62 [1,3,2,3], 64 [1,3, 3,3], 65 [2,3,3,3],

66 [3,3,3,3], 79 [3,3,4,3], 80 [3,3,4,4], 81 [4,3,4,4], 93 [4,3, 4,5]

Esta solución fusionada permite una consulta en el tiempo O (log n  +  k ): simplemente busque q en L y luego informe los resultados almacenados en el elemento x encontrado por esta búsqueda. Por ejemplo, si q = 50, al buscar q en L se encuentra el elemento 62 [1,3,2,3], del cual devolvemos los resultados L ₁ [1] = 64, L ₂ [3] (un valor de marca indicando que q está más allá del final de L ₂ ), L ₃ [2] = 62 y L ₄ [3] = 79. Sin embargo, esta solución paga una alta penalización en la complejidad del espacio: usa el espacio O ( kn ) como cada de los n elementos en L deben almacenar una lista de k resultados de búsqueda.

La cascada fraccionada permite resolver este mismo problema de búsqueda con límites de tiempo y espacio que satisfacen lo mejor de ambos mundos: tiempo de consulta O (log n  +  k ) y espacio O ( n ). La solución en cascada fraccionada es almacenar una nueva secuencia de listas M _i . La lista final de esta secuencia, M _k , es igual a L _k ; cada lista anterior M _i se forma fusionando L _i con cada segundo elemento de M _{i +1} . Con cada elemento x en esta lista combinada, almacenamos dos números: la posición resultante de buscar x en L _i y la posición resultante de buscar x en M _{i +1} . Para los datos anteriores, esto nos daría las siguientes listas:

M ₁ = 24 [0, 1], 25 [1, 1], 35 [1, 3], 64 [1, 5], 65 [2, 5], 79 [3, 5], 80 [3, 6 ], 93 [4, 6]

M ₂ = 23 [0, 1], 25 [1, 1], 26 [2, 1], 35 [3, 1], 62 [3, 3], 79 [3, 5]

M ₃ = 13 [0, 1], 35 [1, 1], 44 [1, 2], 62 [2, 3], 66 [3, 3], 79 [4, 3]

M ₄ = 11 [0, 0], 35 [1, 0], 46 [2, 0], 79 [3, 0], 81 [4, 0]

Supongamos que deseamos realizar una consulta en esta estructura, para q = 50. Primero hacemos una búsqueda binaria estándar para q en M ₁ , encontrando el valor 64 [1,5]. El "1" en 64 [1,5], nos dice que la búsqueda de q en L ₁ debería devolver L ₁ [1] = 64. El "5" en 64 [1,5] nos dice que la ubicación aproximada de q en M ₂ es la posición 5. Más precisamente, la búsqueda binaria de q en M ₂ devolvería el valor 79 [3,5] en la posición 5, o el valor 62 [3,3] un lugar antes. Comparando q con 62, y observando que es más pequeño, determinamos que el resultado de búsqueda correcto en M ₂ es 62 [3,3]. El primer "3" en 62 [3,3] nos dice que la búsqueda de q en L ₂ debería devolver L ₂ [3], un valor de bandera que significa que q está más allá del final de la lista L ₂ . El segundo "3" en 62 [3,3] nos dice que la ubicación aproximada de q en M ₃ es la posición 3. Más precisamente, la búsqueda binaria de q en M ₃ devolvería el valor 62 [2,3] en la posición 3, o el valor 44 [1,2] un lugar antes. Una comparación de q con el valor más pequeño 44 nos muestra que el resultado de búsqueda correcto en M ₃ es 62 [2,3]. El "2" en 62 [2,3] nos dice que la búsqueda de q en L ₃ debería devolver L ₃ [2] = 62, y el "3" en 62 [2,3] nos dice que el resultado de la búsqueda para q en M ₄ es M ₄ [3] = 79 [3,0] o M ₄ [2] = 46 [2,0]; comparar q con 46 muestra que el resultado correcto es 79 [3,0] y que el resultado de buscar q en L ₄ es L ₄ [3] = 79. Por lo tanto, hemos encontrado q en cada una de nuestras cuatro listas, por haciendo una búsqueda binaria en la lista única M ₁ seguida de una única comparación en cada una de las listas sucesivas.

De manera más general, para cualquier estructura de datos de este tipo, realizamos una consulta haciendo una búsqueda binaria de q en M ₁ y determinando a partir del valor resultante la posición de q en L ₁ . Entonces, para cada i > 1, usamos la posición conocida de q en M _i para encontrar su posición en M _{i +1} . El valor asociado con la posición de q en M _i apunta a una posición en M _{i +1} que es el resultado correcto de la búsqueda binaria de q en M _{i +1} o está a un solo paso de ese resultado correcto, por lo que avanzando de i a i  + 1 requiere una sola comparación. Por tanto, el tiempo total de una consulta es O (log n  +  k ).

En nuestro ejemplo, las listas fraccionadas en cascada tienen un total de 25 elementos, menos del doble que la entrada original. En general, el tamaño de M _i en esta estructura de datos es como máximo

${\ Displaystyle | L_ {i} | + {\ frac {1} {2}} | L_ {i + 1} | + {\ frac {1} {4}} | L_ {i + 2} | + \ cdots + {\ frac {1} {2 ^ {j}}} | L_ {i + j} | + \ cdots,}$

como puede demostrarse fácilmente por inducción. Por lo tanto, el tamaño total de la estructura de datos es como máximo

${\ Displaystyle \ sum | M_ {i} | = \ sum | L_ {i} | \ left (1 + {\ frac {1} {2}} + {\ frac {1} {4}} + \ cdots \ derecha) \ leq 2n = O (n),}$

como puede verse reagrupando las contribuciones al tamaño total provenientes de la misma lista de entrada L _i juntas.

El problema general

En general, la cascada fraccional comienza con un gráfico de catálogo , un gráfico dirigido en el que cada vértice está etiquetado con una lista ordenada. Una consulta en esta estructura de datos consta de una ruta en el gráfico y un valor de consulta q ; la estructura de datos debe determinar la posición de q en cada una de las listas ordenadas asociadas a los vértices del camino. Para el ejemplo simple anterior, el gráfico del catálogo es en sí mismo una ruta, con solo cuatro nodos. Es posible que los vértices posteriores en la ruta se determinen dinámicamente como parte de una consulta, en respuesta a los resultados encontrados por las búsquedas en partes anteriores de la ruta.

Para manejar consultas de este tipo, para un gráfico en el que cada vértice tiene como máximo d bordes entrantes y como máximo d salientes para alguna constante d , las listas asociadas con cada vértice se incrementan en una fracción de los elementos de cada vecino saliente del vértice; la fracción debe elegirse para que sea menor que 1 / d , de modo que la cantidad total por la que se aumentan todas las listas permanezca lineal en el tamaño de entrada. Cada elemento de cada lista aumentada almacena con él la posición de ese elemento en la lista no aumentada almacenada en el mismo vértice y en cada una de las listas vecinas salientes. En el ejemplo simple anterior, d = 1, y aumentamos cada lista con 1/2 fracción de los elementos vecinos.

Una consulta en esta estructura de datos consiste en una búsqueda binaria estándar en la lista aumentada asociada con el primer vértice de la ruta de consulta, junto con búsquedas más simples en cada vértice sucesivo de la ruta. Si se usa una fracción de 1 / r de elementos para aumentar las listas de cada elemento vecino, entonces cada resultado de consulta sucesiva se puede encontrar dentro de, como máximo, r pasos de la posición almacenada en el resultado de la consulta del vértice de la ruta anterior y, por lo tanto, puede ser encontrado en tiempo constante sin tener que realizar una búsqueda binaria completa.

Cascada fraccionada dinámica

En la cascada fraccionada dinámica , la lista almacenada en cada nodo del gráfico del catálogo puede cambiar dinámicamente, mediante una secuencia de actualizaciones en las que se insertan y eliminan elementos de la lista. Esto provoca varias dificultades para la estructura de datos.

Primero, cuando un elemento se inserta o elimina en un nodo del gráfico del catálogo, debe colocarse dentro de la lista aumentada asociada con ese nodo y puede causar que los cambios se propaguen a otros nodos del gráfico del catálogo. En lugar de almacenar las listas aumentadas en matrices, deben almacenarse como árboles de búsqueda binarios, de modo que estos cambios se puedan manejar de manera eficiente y al mismo tiempo permitir búsquedas binarias de las listas aumentadas.

En segundo lugar, una inserción o eliminación puede provocar un cambio en el subconjunto de la lista asociado con un nodo que se pasa a los nodos vecinos del gráfico de catálogo. Ya no es factible, en el entorno dinámico, que este subconjunto se elija como los elementos en cada d- ésima posición de la lista, para algunos d , ya que este subconjunto cambiaría demasiado drásticamente después de cada actualización. Más bien, una técnica estrechamente relacionada con los árboles B permite la selección de una fracción de datos que se garantiza que sea menor que 1 / d , con la garantía de que los elementos seleccionados estarán espaciados en un número constante de posiciones en la lista completa, y tal que una inserción o eliminación en la lista aumentada asociada con un nodo hace que los cambios se propaguen a otros nodos para una fracción de las operaciones que es menor que 1 / d . De esta forma, la distribución de los datos entre los nodos satisface las propiedades necesarias para que el algoritmo de consulta sea rápido, garantizando al mismo tiempo que el número medio de operaciones del árbol de búsqueda binaria por inserción o eliminación de datos sea constante.

En tercer lugar, y lo que es más crítico, la estructura de datos en cascada fraccional estática mantiene, para cada elemento x de la lista aumentada en cada nodo del gráfico del catálogo, el índice del resultado que se obtendría al buscar x entre los elementos de entrada de ese nodo. y entre las listas aumentadas almacenadas en los nodos vecinos. Sin embargo, esta información sería demasiado cara de mantener en el entorno dinámico. Insertar o eliminar un solo valor x podría hacer que los índices almacenados en un número ilimitado de otros valores cambien. En cambio, las versiones dinámicas de cascada fraccionada mantienen varias estructuras de datos para cada nodo:

• Un mapeo de los elementos en la lista aumentada del nodo a pequeños enteros, de modo que el orden de las posiciones en la lista aumentada es equivalente al orden de comparación de los enteros, y un mapeo inverso de estos enteros a los elementos de la lista. Una técnica de Dietz (1982) permite mantener esta numeración de manera eficiente.
• Una estructura de datos de búsqueda de enteros, como un árbol de van Emde Boas, para los números asociados con la lista de entrada del nodo. Con esta estructura, y el mapeo de elementos a enteros, uno puede encontrar de manera eficiente para cada elemento x de la lista aumentada, el elemento que se encontraría al buscar x en la lista de entrada.
• Para cada nodo vecino en el gráfico de catálogo, una estructura de datos de búsqueda de enteros similar para los números asociados con el subconjunto de datos propagados desde el nodo vecino. Con esta estructura, y el mapeo de elementos a números enteros, uno puede encontrar eficientemente para cada elemento x de la lista aumentada, una posición dentro de un número constante de pasos de la ubicación de x en la lista aumentada asociada con el nodo vecino.

Estas estructuras de datos permiten realizar una cascada fraccional dinámica en un momento de O (log  n ) por inserción o eliminación, y realizar una secuencia de k búsquedas binarias siguiendo una ruta de longitud k en el gráfico de catálogo en el tiempo O (log  n  +  k  log log  n ).

Aplicaciones

Las capas convexas de un conjunto de puntos, parte de una estructura de datos en cascada fraccionada eficiente para informes de rango de medio plano.

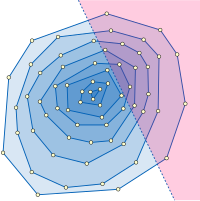
Las aplicaciones típicas de la cascada fraccionada involucran estructuras de datos de búsqueda de rango en geometría computacional . Por ejemplo, considere el problema de los informes de rango de semiplano : es decir, intersecar un conjunto fijo de n puntos con un semiplano de consulta y enumerar todos los puntos en la intersección. El problema es estructurar los puntos de tal manera que una consulta de este tipo pueda ser respondida de manera eficiente en términos del tamaño de la intersección h . Una estructura que se puede utilizar para este propósito son las capas convexas del conjunto de puntos de entrada, una familia de polígonos convexos anidados que consta del casco convexo del conjunto de puntos y las capas convexas construidas recursivamente de los puntos restantes. Dentro de una sola capa, los puntos dentro del semiplano de la consulta se pueden encontrar realizando una búsqueda binaria de la pendiente de la línea de límite del semiplano entre la secuencia ordenada de pendientes convexas de los bordes del polígono, lo que lleva al vértice del polígono que se encuentra dentro de la mitad de la consulta. -plane y el más alejado de su límite, y luego buscar secuencialmente a lo largo de los bordes del polígono para encontrar todos los demás vértices dentro del semiplano de consulta. Todo el problema del informe de rango de semiplano puede resolverse repitiendo este procedimiento de búsqueda comenzando desde la capa más externa y continuando hacia adentro hasta llegar a una capa que está separada del semiespacio de consulta. La cascada fraccionada acelera las búsquedas binarias sucesivas entre las secuencias de pendientes de borde de polígono en cada capa, lo que lleva a una estructura de datos para este problema con el espacio O ( n ) y el tiempo de consulta O (log  n  +  h ). La estructura de datos se puede construir en el tiempo O ( n  log  n ) mediante un algoritmo de Chazelle (1985) . Como en nuestro ejemplo, esta aplicación implica búsquedas binarias en una secuencia lineal de listas (la secuencia anidada de las capas convexas), por lo que el gráfico del catálogo es solo una ruta.

Otra aplicación de la cascada fraccionada en estructuras de datos geométricos se refiere a la ubicación de puntos en una subdivisión monótona, es decir, una partición del plano en polígonos de manera que cualquier línea vertical interseca cualquier polígono en como máximo dos puntos. Como demostraron Edelsbrunner, Guibas y Stolfi (1986) , este problema se puede resolver encontrando una secuencia de caminos poligonales que se extienden de izquierda a derecha a través de la subdivisión, y buscando binariamente el más bajo de estos caminos que esté por encima del punto de consulta. Probar si el punto de consulta está por encima o por debajo de una de las rutas se puede resolver en sí mismo como un problema de búsqueda binaria, buscando la coordenada x de los puntos entre las coordenadas x de los vértices de la ruta para determinar qué borde de la ruta podría estar por encima o por debajo de la punto de consulta. Por lo tanto, cada consulta de ubicación de punto se puede resolver como una capa externa de búsqueda binaria entre las rutas, cada paso de la cual realiza una búsqueda binaria entre las coordenadas x de los vértices. La cascada fraccionada se puede utilizar para acelerar el tiempo de las búsquedas binarias internas, reduciendo el tiempo total por consulta a O (log  n ) utilizando una estructura de datos con espacio O ( n ). En esta aplicación, el gráfico del catálogo es un árbol que representa las posibles secuencias de búsqueda de la búsqueda binaria externa.

Más allá de la geometría computacional, Lakshman y Stiliadis (1998) y Buddhikot, Suri y Waldvogel (1999) aplican la cascada fraccionada en el diseño de estructuras de datos para el filtrado rápido de paquetes en enrutadores de Internet . Gao y col. (2004) utilizan la cascada fraccionada como modelo para la distribución y recuperación de datos en redes de sensores .

Referencias