Valores propios y vectores propios - Eigenvalues and eigenvectors

En álgebra lineal , un vector propio ( / aɪ ɡ ə n ˌ v ɛ k t ər / ) o vector característico de una transformación lineal es un no nulo vector que los cambios en la mayoría por un escalar factor al que la transformación lineal se aplica a ella. El valor propio correspondiente , a menudo denotado por , es el factor por el cual se escala el vector propio. ${\ Displaystyle \ lambda}$

Geométricamente , un autovector, correspondiente a un autovalor real distinto de cero, apunta en una dirección en la que se estira por la transformación y el autovalor es el factor por el cual se estira. Si el valor propio es negativo, la dirección se invierte. Hablando libremente, en un espacio vectorial multidimensional , el vector propio no se rota.

Definicion formal

Si $T$ es una transformación lineal de un espacio vectorial $V$ sobre un campo $F$ en sí mismo $yv$ es un vector distinto de cero en $V$ , entonces $v$ es un vector propio de $T$ si $T (v)$ es un múltiplo escalar de $v$ . Esto se puede escribir como

{\ Displaystyle T (\ mathbf {v}) = \ lambda \ mathbf {v},}

donde $λ$ es un escalar en $F$ , conocido como valor propio , valor característico o raíz característica asociada con $v$ .

Existe una correspondencia directa entre n- por- n matrices cuadradas y transformaciones lineales de un espacio vectorial n- dimensional en sí mismo, dada cualquier base del espacio vectorial. Por tanto, en un espacio vectorial de dimensión finita, es equivalente a definir valores propios y vectores propios utilizando el lenguaje de matrices o el lenguaje de transformaciones lineales.

Si $V$ es de dimensión finita, la ecuación anterior es equivalente a

{\ Displaystyle A \ mathbf {u} = \ lambda \ mathbf {u}.}

donde $A$ es la representación matricial de $T$ y $T$ es el vector de coordenadas de $v$ .

Visión general

Los autovalores y autovectores ocupan un lugar destacado en el análisis de transformaciones lineales. El prefijo eigen- se adopta de la palabra alemana eigen ( análoga a la palabra inglesa propia ) para "propio", "característico", "propio". Originalmente utilizados para estudiar los ejes principales del movimiento de rotación de cuerpos rígidos , los valores propios y los vectores propios tienen una amplia gama de aplicaciones, por ejemplo, en análisis de estabilidad , análisis de vibraciones , orbitales atómicos , reconocimiento facial y diagonalización de matrices .

En esencia, un vector propio v de una transformación lineal T es un vector distinto de cero que, cuando se le aplica T , no cambia de dirección. La aplicación de T al autovector solo escala el autovector por el valor escalar λ , llamado autovalor. Esta condición se puede escribir como la ecuación

{\ Displaystyle T (\ mathbf {v}) = \ lambda \ mathbf {v},}

denominada ecuación de valor propio o ecuación propia . En general, λ puede ser cualquier escalar . Por ejemplo, λ puede ser negativo, en cuyo caso el vector propio invierte la dirección como parte de la escala, o puede ser cero o complejo .

En este mapeo de corte, la flecha roja cambia de dirección, pero la flecha azul no. La flecha azul es un vector propio de este mapeo de corte porque no cambia de dirección, y dado que su longitud no cambia, su valor propio es 1.

Una matriz simétrica y real de 2 × 2 representa un estiramiento y un corte del plano. Los vectores propios de la matriz (líneas rojas) son las dos direcciones especiales, de modo que cada punto de ellos simplemente se deslizará sobre ellos.

El ejemplo de Mona Lisa que se muestra aquí proporciona una ilustración simple. Cada punto de la pintura se puede representar como un vector que apunta desde el centro de la pintura a ese punto. La transformación lineal en este ejemplo se llama mapeo de corte . Los puntos en la mitad superior se mueven hacia la derecha y los puntos en la mitad inferior se mueven hacia la izquierda, proporcionalmente a lo lejos que están del eje horizontal que pasa por el centro de la pintura. Por lo tanto, los vectores que apuntan a cada punto de la imagen original se inclinan hacia la derecha o hacia la izquierda, y la transformación los hace más largos o más cortos. Los puntos a lo largo del eje horizontal no se mueven en absoluto cuando se aplica esta transformación. Por lo tanto, cualquier vector que apunte directamente a la derecha o izquierda sin componente vertical es un vector propio de esta transformación, porque el mapeo no cambia su dirección. Además, todos estos autovectores tienen un autovalor igual a uno, porque el mapeo tampoco cambia su longitud.

Las transformaciones lineales pueden tomar muchas formas diferentes, mapeando vectores en una variedad de espacios vectoriales, por lo que los vectores propios también pueden tomar muchas formas. Por ejemplo, la transformación lineal podría ser un operador diferencial como , en cuyo caso los vectores propios son funciones llamadas funciones propias que son escaladas por ese operador diferencial, como ${\ displaystyle {\ tfrac {d} {dx}}}$

{\ Displaystyle {\ frac {d} {dx}} e ^ {\ lambda x} = \ lambda e ^ {\ lambda x}.}

Alternativamente, la transformación lineal podría tomar la forma de una matriz de n por n , en cuyo caso los vectores propios son matrices de n por 1. Si la transformación lineal se expresa en forma de una matriz A de n por n , entonces la ecuación de valor propio para una transformación lineal anterior se puede reescribir como la multiplicación de matrices

{\ Displaystyle A \ mathbf {v} = \ lambda \ mathbf {v},}

donde el vector propio v es una matriz de n por 1. Para una matriz, los valores propios y los vectores propios se pueden utilizar para descomponer la matriz, por ejemplo, diagonalizándola .

Los valores propios y los vectores propios dan lugar a muchos conceptos matemáticos estrechamente relacionados, y el prefijo eigen- se aplica libremente al nombrarlos:

El conjunto de todos los vectores propios de una transformación lineal, cada uno emparejado con su valor propio correspondiente, se denomina sistema propio de esa transformación.
El conjunto de todos los autovectores de T correspondientes al mismo autovalor, junto con el vector cero, se llama un autoespacio , o el espacio característico de T asociado con ese autovalor.
Si un conjunto de autovectores de T forma una base del dominio de T , entonces esta base se llama autobasis .

Historia

Los valores propios a menudo se introducen en el contexto del álgebra lineal o la teoría de matrices . Sin embargo, históricamente surgieron en el estudio de formas cuadráticas y ecuaciones diferenciales .

En el siglo XVIII, Leonhard Euler estudió el movimiento de rotación de un cuerpo rígido y descubrió la importancia de los ejes principales . Joseph-Louis Lagrange se dio cuenta de que los ejes principales son los vectores propios de la matriz de inercia.

A principios del siglo XIX, Augustin-Louis Cauchy vio cómo su trabajo podía usarse para clasificar las superficies cuádricas y lo generalizó a dimensiones arbitrarias. Cauchy también acuñó el término racine caractéristique (raíz característica), para lo que ahora se llama valor propio ; su término sobrevive en ecuación característica .

Más tarde, Joseph Fourier utilizó el trabajo de Lagrange y Pierre-Simon Laplace para resolver la ecuación de calor mediante la separación de variables en su famoso libro de 1822 Théorie analytique de la chaleur . Charles-François Sturm desarrolló aún más las ideas de Fourier y las llamó la atención de Cauchy, quien las combinó con sus propias ideas y llegó al hecho de que las matrices simétricas reales tienen valores propios reales. Esto fue ampliado por Charles Hermite en 1855 a lo que ahora se llaman matrices hermitianas .

Casi al mismo tiempo, Francesco Brioschi demostró que los valores propios de las matrices ortogonales se encuentran en el círculo unitario , y Alfred Clebsch encontró el resultado correspondiente para las matrices asimétricas asimétricas . Finalmente, Karl Weierstrass aclaró un aspecto importante en la teoría de la estabilidad iniciada por Laplace, al darse cuenta de que las matrices defectuosas pueden causar inestabilidad.

Mientras tanto, Joseph Liouville estudió problemas de valores propios similares a los de Sturm; la disciplina que surgió de su trabajo ahora se llama teoría de Sturm-Liouville . Schwarz estudió el primer valor propio de la ecuación de Laplace en dominios generales hacia finales del siglo XIX, mientras que Poincaré estudió la ecuación de Poisson unos años más tarde.

A principios del siglo XX, David Hilbert estudió los valores propios de los operadores integrales al considerarlos como matrices infinitas. Fue el primero en usar la palabra alemana eigen , que significa "propio", para denotar autovalores y autovectores en 1904, aunque pudo haber estado siguiendo un uso relacionado de Hermann von Helmholtz . Durante algún tiempo, el término estándar en inglés fue "valor adecuado", pero el término más distintivo "valor propio" es el estándar en la actualidad.

El primer algoritmo numérico para calcular valores propios y vectores propios apareció en 1929, cuando Richard von Mises publicó el método de potencia . Uno de los métodos más populares en la actualidad, el algoritmo QR , fue propuesto de forma independiente por John GF Francis y Vera Kublanovskaya en 1961.

Autovalores y autovectores de matrices

Los valores propios y los vectores propios a menudo se presentan a los estudiantes en el contexto de cursos de álgebra lineal centrados en matrices. Además, las transformaciones lineales sobre un espacio vectorial de dimensión finita se pueden representar mediante matrices, lo que es especialmente común en aplicaciones numéricas y computacionales.

Matrix A actúa estirando el vector x , no cambiando su dirección, por lo que x es un vector propio de A .

Considere los vectores $n-$ dimensionales que se forman como una lista de $n$ escalares, como los vectores tridimensionales

{\ Displaystyle \ mathbf {x} = {\ begin {bmatrix} 1 \\ - 3 \\ 4 \ end {bmatrix}} \ quad {\ mbox {y}} \ quad \ mathbf {y} = {\ begin { bmatrix} -20 \\ 60 \\ - 80 \ end {bmatrix}}.}

Se dice que estos vectores son múltiplos escalares entre sí, o paralelos o colineales , si hay un escalar $λ$ tal que

{\ Displaystyle \ mathbf {x} = \ lambda \ mathbf {y}.}

En este caso . ${\ Displaystyle \ lambda = - {\ frac {1} {20}}}$

Ahora considere la transformación lineal de vectores $n-$ dimensionales definidos por una matriz $A de$ $n$ por $n$ ,

{\ Displaystyle A \ mathbf {v} = \ mathbf {w},}

o

{\ displaystyle {\ begin {bmatrix} A_ {11} & A_ {12} & \ cdots & A_ {1n} \\ A_ {21} & A_ {22} & \ cdots & A_ {2n} \\\ vdots & \ vdots & \ ddots & \ vdots \\ A_ {n1} & A_ {n2} & \ cdots & A_ {nn} \\\ end {bmatrix}} {\ begin {bmatrix} v_ {1} \\ v_ {2} \\\ vdots \ \ v_ {n} \ end {bmatrix}} = {\ begin {bmatrix} w_ {1} \\ w_ {2} \\\ vdots \\ w_ {n} \ end {bmatrix}}}

donde, para cada fila,

{\ Displaystyle w_ {i} = A_ {i1} v_ {1} + A_ {i2} v_ {2} + \ cdots + A_ {in} v_ {n} = \ sum _ {j = 1} ^ {n} A_ {ij} v_ {j}.}

Si ocurre que $v$ y $w$ son múltiplos escalares, eso es si

{\ Displaystyle A \ mathbf {v} = \ mathbf {w} = \ lambda \ mathbf {v},}

( 1 )

entonces $v$ es un autovector de la transformación lineal $A$ y el factor de escala $λ$ es el autovalor correspondiente a ese autovector. La ecuación ( 1 ) es la ecuación de valores propios para la matriz $A$ .

La ecuación ( 1 ) puede expresarse de manera equivalente como

{\ Displaystyle \ left (A- \ lambda I \ right) \ mathbf {v} = \ mathbf {0},}

( 2 )

donde $I$ es la matriz identidad $n$ por $n$ y 0 es el vector cero.

Autovalores y el polinomio característico

La ecuación ( 2 ) tiene una solución distinta de cero v si y solo si el determinante de la matriz ( A - λI ) es cero. Por tanto, los autovalores de A son valores de λ que satisfacen la ecuación

{\ Displaystyle | A- \ lambda I | = 0}

( 3 )

Utilizando la regla de Leibniz para el determinante, el lado izquierdo de la ecuación ( 3 ) es un polinomio en función de la variable λ y el grado de este polinomio se n , el orden de la matriz A . Sus coeficientes dependen de las entradas de A , excepto que su término de grado n es siempre (−1) ⁿ λ ⁿ . Este polinomio se llama el polinomio característico de A . La ecuación ( 3 ) se llama la ecuación característica o la ecuación secular de A .

El teorema fundamental del álgebra implica que el polinomio característico de una matriz de n- por- n A , siendo un polinomio de grado n , se puede factorizar en el producto de n términos lineales,

{\ Displaystyle | A- \ lambda I | = (\ lambda _ {1} - \ lambda) (\ lambda _ {2} - \ lambda) \ cdots (\ lambda _ {n} - \ lambda),}

( 4 )

donde cada λ _i puede ser real pero en general es un número complejo. Los números lambda ₁ , λ ₂ , ..., λ _n , que no pueden tener todos los valores distintos, son las raíces del polinomio y son los valores propios de A .

Como un breve ejemplo, que se describe con más detalle en la sección de ejemplos más adelante, considere la matriz

{\ displaystyle A = {\ begin {bmatrix} 2 & 1 \\ 1 & 2 \ end {bmatrix}}.}

Tomando el determinante de ( A - λI ) , el polinomio característico de A es

{\ displaystyle | A- \ lambda I | = {\ begin {vmatrix} 2- \ lambda & 1 \\ 1 & 2- \ lambda \ end {vmatrix}} = 3-4 \ lambda + \ lambda ^ {2}.}

Ajuste de las raíces polinomio característico igual a cero, que tiene a λ = 1 y λ = 3 , que son los dos valores propios de A . Los autovectores correspondientes a cada autovalor se pueden encontrar resolviendo los componentes de v en la ecuación . En este ejemplo, los vectores propios son cualquier múltiplo escalar distinto de cero de ${\ Displaystyle \ left (A- \ lambda I \ right) \ mathbf {v} = \ mathbf {0}}$

{\ Displaystyle \ mathbf {v} _ {\ lambda = 1} = {\ begin {bmatrix} 1 \\ - 1 \ end {bmatrix}}, \ quad \ mathbf {v} _ {\ lambda = 3} = { \ begin {bmatrix} 1 \\ 1 \ end {bmatrix}}.}

Si las entradas de la matriz A son todas números reales, entonces los coeficientes del polinomio característico también serán números reales, pero los valores propios aún pueden tener partes imaginarias distintas de cero. Por tanto, las entradas de los vectores propios correspondientes también pueden tener partes imaginarias distintas de cero. De manera similar, los valores propios pueden ser números irracionales incluso si todas las entradas de A son números racionales o incluso si son todos enteros. Sin embargo, si las entradas de A son todos números algebraicos , que incluyen los racionales, los valores propios son números algebraicos complejos.

Las raíces no reales de un polinomio real con coeficientes reales se pueden agrupar en pares de conjugados complejos , es decir, los dos miembros de cada par tienen partes imaginarias que solo difieren en el signo y la misma parte real. Si el grado es impar, entonces, según el teorema del valor intermedio, al menos una de las raíces es real. Por lo tanto, cualquier matriz real con orden impar tiene al menos un valor propio real, mientras que una matriz real con orden par puede no tener valores propios reales. Los vectores propios asociados con estos valores propios complejos también son complejos y también aparecen en pares conjugados complejos.

Multiplicidad algebraica

Sea λ _i un valor propio de una matriz A de n por n . La multiplicidad algebraica μ _A ( λ _i ) del valor propio es su multiplicidad como raíz del polinomio característico, es decir, el entero más grande k tal que ( λ - λ _i ) ^k divide uniformemente ese polinomio.

Supongamos que una matriz A tiene dimensión n y d ≤ n valores propios distintos. Mientras que la ecuación ( 4 ) factoriza el polinomio característico de A en el producto de n términos lineales con algunos términos potencialmente repetidos, el polinomio característico puede escribirse como el producto de d términos, cada uno correspondiente a un valor propio distinto y elevado a la potencia del multiplicidad algebraica,

{\ Displaystyle | A- \ lambda I | = (\ lambda _ {1} - \ lambda) ^ {\ mu _ {A} (\ lambda _ {1})} (\ lambda _ {2} - \ lambda) ^ {\ mu _ {A} (\ lambda _ {2})} \ cdots (\ lambda _ {d} - \ lambda) ^ {\ mu _ {A} (\ lambda _ {d})}.}

Si d = n, entonces el lado derecho es el producto de n términos lineales y esto es lo mismo que la Ecuación ( 4 ). El tamaño de la multiplicidad algebraica de cada valor propio está relacionado con la dimensión n como

{\ Displaystyle {\ begin {alineado} 1 & \ leq \ mu _ {A} (\ lambda _ {i}) \ leq n, \\\ mu _ {A} & = \ sum _ {i = 1} ^ { d} \ mu _ {A} \ left (\ lambda _ {i} \ right) = n. \ end {alineado}}}

Si μ _A ( λ _i ) = 1, entonces se dice que λ _i es un valor propio simple . Si μ _A ( λ _i ) es igual a la multiplicidad geométrica de λ _i , γ _A ( λ _i ), definida en la siguiente sección, entonces se dice que λ _i es un valor propio semisimple .

Espacios propios, multiplicidad geométrica y base propia para matrices

Dado un valor propio particular λ de la matriz A de n por n , defina el conjunto E como todos los vectores v que satisfacen la Ecuación ( 2 ),

{\ Displaystyle E = \ left \ {\ mathbf {v}: \ left (A- \ lambda I \ right) \ mathbf {v} = \ mathbf {0} \ right \}.}

Por un lado, este conjunto es precisamente el núcleo o espacio nulo de la matriz ( A - λI ). Por otra parte, por definición, cualquier vector distinto de cero que satisfaga esta condición es un vector propio de A asociado con λ . Entonces, el conjunto E es la unión del vector cero con el conjunto de todos los autovectores de A asociados con λ , y E es igual al espacio nulo de ( A - λI ). E se denomina espacio propio o espacio característico de A asociado con λ . En general, λ es un número complejo y los vectores propios son matrices complejas de n por 1. Una propiedad del espacio nulo es que es un subespacio lineal , por lo que E es un subespacio lineal de ℂ ⁿ .

Debido a que el autoespacio E es un subespacio lineal, está cerrado bajo adición. Es decir, si dos vectores u y v pertenecen al conjunto E , escrito u , v ∈ E , entonces ( u + v ) ∈ E o equivalentemente A ( u + v ) = λ ( u + v ) . Esto se puede verificar usando la propiedad distributiva de la multiplicación de matrices. De manera similar, debido a que E es un subespacio lineal, está cerrado bajo la multiplicación escalar. Es decir, si v ∈ E y α es un número complejo, ( α v ) ∈ E o equivalentemente A ( α v ) = λ ( α v ) . Esto puede comprobarse observando que la multiplicación de matrices complejas por números complejos es conmutativa . Mientras u + v y α v no son cero, sino que también son vectores propios de A asociados con λ .

La dimensión del espacio propio E asociado con λ , o de forma equivalente, el número máximo de vectores propios linealmente independientes asociados con λ , se denomina multiplicidad geométrica del valor propio γ _A ( λ ). Debido a que E también es el espacio nulo de ( A - λI ), la multiplicidad geométrica de λ es la dimensión del espacio nulo de ( A - λI ), también llamado nulidad de ( A - λI ), que se relaciona con la dimensión y rango de ( A - λI ) como

{\ Displaystyle \ gamma _ {A} (\ lambda) = n- \ operatorname {rango} (A- \ lambda I).}

Debido a la definición de autovalores y autovectores, la multiplicidad geométrica de un autovalor debe ser al menos uno, es decir, cada autovalor tiene al menos un autovector asociado. Además, la multiplicidad geométrica de un valor propio no puede exceder su multiplicidad algebraica. Además, recuerde que la multiplicidad algebraica de un valor propio no puede exceder n .

{\ Displaystyle 1 \ leq \ gamma _ {A} (\ lambda) \ leq \ mu _ {A} (\ lambda) \ leq n}

Para probar la desigualdad , considere cómo la definición de multiplicidad geométrica implica la existencia de vectores propios ortonormales , tales que . Por lo tanto, podemos encontrar una matriz (unitaria) cuyas primeras columnas son estos autovectores, y cuyas columnas restantes pueden ser cualquier conjunto ortonormal de vectores ortogonales a estos autovectores de . Entonces tiene rango completo y por lo tanto es invertible, y con una matriz cuyo bloque superior izquierdo es la matriz diagonal . Esto implica eso . En otras palabras, es similar a , lo que implica eso . Pero por la definición de sabemos que contiene un factor , lo que significa que la multiplicidad algebraica de debe satisfacer . ${\ Displaystyle \ gamma _ {A} (\ lambda) \ leq \ mu _ {A} (\ lambda)}$ ${\ Displaystyle \ gamma _ {A} (\ lambda)}$ ${\ displaystyle {\ boldsymbol {v}} _ {1}, \, \ ldots, \, {\ boldsymbol {v}} _ {\ gamma _ {A} (\ lambda)}}$ ${\ displaystyle A {\ boldsymbol {v}} _ {k} = \ lambda {\ boldsymbol {v}} _ {k}}$ ${\ Displaystyle V}$ ${\ Displaystyle \ gamma _ {A} (\ lambda)}$ ${\ Displaystyle n- \ gamma _ {A} (\ lambda)}$ ${\ Displaystyle A}$ ${\ Displaystyle V}$ ${\ Displaystyle AV = VD}$ ${\ Displaystyle D}$ ${\ Displaystyle \ lambda I _ {\ gamma _ {A} (\ lambda)}}$ ${\ Displaystyle (A- \ xi yo) V = V (D- \ xi yo)}$ ${\ Displaystyle A- \ xi I}$ ${\ Displaystyle D- \ xi I}$ ${\ Displaystyle \ det (A- \ xi yo) = \ det (D- \ xi yo)}$ ${\ Displaystyle D}$ ${\ Displaystyle \ det (D- \ xi I)}$ ${\ Displaystyle (\ xi - \ lambda) ^ {\ gamma _ {A} (\ lambda)}}$ ${\ Displaystyle \ lambda}$ ${\ Displaystyle \ mu _ {A} (\ lambda) \ geq \ gamma _ {A} (\ lambda)}$

Supongamos que tiene valores propios distintos , donde la multiplicidad geométrica de es . La multiplicidad geométrica total de , ${\ Displaystyle A}$ ${\ Displaystyle d \ leq n}$ ${\ Displaystyle \ lambda _ {1}, \ ldots, \ lambda _ {d}}$ ${\ Displaystyle \ lambda _ {i}}$ ${\ Displaystyle \ gamma _ {A} (\ lambda _ {i})}$ ${\ Displaystyle A}$

{\ Displaystyle {\ begin {alineado} \ gamma _ {A} & = \ sum _ {i = 1} ^ {d} \ gamma _ {A} (\ lambda _ {i}), \\ d & \ leq \ gamma _ {A} \ leq n, \ end {alineado}}}

es la dimensión de la suma de todos los espacios propios de los valores propios de, o, de manera equivalente, el número máximo de vectores propios linealmente independientes de . Si entonces ${\ Displaystyle A}$ ${\ Displaystyle A}$ ${\ Displaystyle \ gamma _ {A} = n}$

La suma directa de los espacios propios de todos los valores propios es el espacio vectorial completo . ${\ Displaystyle A}$ ${\ Displaystyle \ mathbb {C} ^ {n}}$
Se puede formar una base de a partir de autovectores linealmente independientes de ; tal base se llama eigenbasis ${\ Displaystyle \ mathbb {C} ^ {n}}$ ${\ Displaystyle n}$ ${\ Displaystyle A}$
Cualquier vector en se puede escribir como una combinación lineal de autovectores de . ${\ Displaystyle \ mathbb {C} ^ {n}}$ ${\ Displaystyle A}$

Propiedades adicionales de los valores propios

Sea una matriz arbitraria de números complejos con valores propios . Cada valor propio aparece veces en esta lista, donde es la multiplicidad algebraica del valor propio. Las siguientes son propiedades de esta matriz y sus valores propios: ${\ Displaystyle A}$ ${\ Displaystyle n \ times n}$ ${\ Displaystyle \ lambda _ {1}, \ ldots, \ lambda _ {n}}$ ${\ Displaystyle \ mu _ {A} (\ lambda _ {i})}$ ${\ Displaystyle \ mu _ {A} (\ lambda _ {i})}$

La traza de , definida como la suma de sus elementos diagonales, es también la suma de todos los valores propios, ${\ Displaystyle A}$
${\ Displaystyle \ operatorname {tr} (A) = \ sum _ {i = 1} ^ {n} a_ {ii} = \ sum _ {i = 1} ^ {n} \ lambda _ {i} = \ lambda _ {1} + \ lambda _ {2} + \ cdots + \ lambda _ {n}.}$
El determinante de es el producto de todos sus valores propios, ${\ Displaystyle A}$
${\ Displaystyle \ det (A) = \ prod _ {i = 1} ^ {n} \ lambda _ {i} = \ lambda _ {1} \ lambda _ {2} \ cdots \ lambda _ {n}.}$
Los autovalores del ^th poder de ; es decir, los valores propios de , para cualquier entero positivo , son . ${\ Displaystyle k}$ ${\ Displaystyle A}$ ${\ Displaystyle A ^ {k}}$ ${\ Displaystyle k}$ ${\ Displaystyle \ lambda _ {1} ^ {k}, \ ldots, \ lambda _ {n} ^ {k}}$
La matriz es invertible si y solo si cada valor propio es distinto de cero. ${\ Displaystyle A}$
Si es invertible, entonces los autovalores de son y la multiplicidad geométrica de cada autovalor coinciden. Además, dado que el polinomio característico de la inversa es el polinomio recíproco del original, los valores propios comparten la misma multiplicidad algebraica. ${\ Displaystyle A}$ ${\ Displaystyle A ^ {- 1}}$ ${\ textstyle {\ frac {1} {\ lambda _ {1}}}, \ ldots, {\ frac {1} {\ lambda _ {n}}}}$
Si es igual a su transpuesta conjugada , o equivalentemente si es hermitiano , entonces cada valor propio es real. Lo mismo ocurre con cualquier matriz real simétrica . ${\ Displaystyle A}$ ${\ Displaystyle A ^ {*}}$ ${\ Displaystyle A}$
Si no solo es hermitiano, sino también positivo-definido , positivo-semidefinito, negativo-definido o negativo-semidefinito, entonces cada valor propio es positivo, no negativo, negativo o no positivo, respectivamente. ${\ Displaystyle A}$
Si es unitario , todo valor propio tiene valor absoluto . ${\ Displaystyle A}$ ${\ Displaystyle | \ lambda _ {i} | = 1}$
si es una matriz y son sus valores propios, entonces los valores propios de la matriz (donde está la matriz identidad) son . Además, si , los valores propios de son . De manera más general, para un polinomio, los valores propios de la matriz son . ${\ Displaystyle A}$ ${\ Displaystyle n \ times n}$ ${\ Displaystyle \ {\ lambda _ {1}, \ ldots, \ lambda _ {k} \}}$ ${\ Displaystyle I + A}$ ${\ Displaystyle I}$ ${\ Displaystyle \ {\ lambda _ {1} +1, \ ldots, \ lambda _ {k} +1 \}}$ ${\ Displaystyle \ alpha \ in \ mathbb {C}}$ ${\ Displaystyle \ alpha I + A}$ ${\ Displaystyle \ {\ lambda _ {1} + \ alpha, \ ldots, \ lambda _ {k} + \ alpha \}}$ ${\ Displaystyle P}$ ${\ Displaystyle P (A)}$ ${\ Displaystyle \ {P (\ lambda _ {1}), \ ldots, P (\ lambda _ {k}) \}}$

Vectores propios izquierdo y derecho

Muchas disciplinas tradicionalmente representan vectores como matrices con una sola columna en lugar de matrices con una sola fila. Por esa razón, la palabra "vector propio" en el contexto de matrices casi siempre se refiere a un vector propio derecho , es decir, un vector columna que multiplica por la derecha la matriz en la ecuación definitoria, Ecuación ( 1 ), ${\ Displaystyle n \ times n}$ ${\ Displaystyle A}$

{\ Displaystyle A \ mathbf {v} = \ lambda \ mathbf {v}.}

El problema de autovalores y autovectores también se puede definir para los vectores de fila que dejaron multiplicar la matriz . En esta formulación, la ecuación definitoria es ${\ Displaystyle A}$

{\ Displaystyle \ mathbf {u} A = \ kappa \ mathbf {u},}

donde es un escalar y es una matriz. Cualquier vector de fila que satisfaga esta ecuación se llama autovector izquierdo de y es su autovalor asociado. Tomando la transpuesta de esta ecuación, ${\ Displaystyle \ kappa}$ ${\ Displaystyle u}$ ${\ Displaystyle 1 \ times n}$ ${\ Displaystyle u}$ ${\ Displaystyle A}$ ${\ Displaystyle \ kappa}$

{\ Displaystyle A ^ {\ textsf {T}} \ mathbf {u} ^ {\ textsf {T}} = \ kappa \ mathbf {u} ^ {\ textsf {T}}.}

Comparando esta ecuación con la Ecuación ( 1 ), se deduce inmediatamente que un autovector izquierdo de es igual que la transpuesta de un autovector derecho de , con el mismo autovalor. Además, dado que el polinomio característico de es el mismo que el polinomio característico de , los autovalores de los autovectores izquierdos de son los mismos que los autovalores de los autovectores derechos de . ${\ Displaystyle A}$ ${\ displaystyle A ^ {\ textsf {T}}}$ ${\ displaystyle A ^ {\ textsf {T}}}$ ${\ Displaystyle A}$ ${\ Displaystyle A}$ ${\ displaystyle A ^ {\ textsf {T}}}$

Diagonalización y autodescomposición

Suponga que los autovectores de A forman una base, o equivalentemente A tiene n autovectores linealmente independientes v ₁ , v ₂ ,…, v _n con autovalores asociados λ ₁ , λ ₂ ,…, λ _n . No es necesario que los valores propios sean distintos. Defina una matriz cuadrada Q cuyas columnas sean los n vectores propios linealmente independientes de A ,

{\ displaystyle Q = {\ begin {bmatrix} \ mathbf {v} _ {1} & \ mathbf {v} _ {2} & \ cdots & \ mathbf {v} _ {n} \ end {bmatrix}}. }

Dado que cada columna de Q es un autovector de A , multiplicando A la derecha por Q se escala cada columna de Q por su autovalor asociado,

{\ Displaystyle AQ = {\ begin {bmatrix} \ lambda _ {1} \ mathbf {v} _ {1} & \ lambda _ {2} \ mathbf {v} _ {2} & \ cdots & \ lambda _ { n} \ mathbf {v} _ {n} \ end {bmatrix}}.}

Con esto en mente, definir un Λ matriz diagonal donde cada elemento Λ diagonal _ii es el valor propio asociado con el i ésima columna de Q . Luego

{\ Displaystyle AQ = Q \ Lambda.}

Debido a que las columnas de Q son linealmente independientes, Q es invertible. A la derecha multiplicando ambos lados de la ecuación por Q ⁻¹ ,

{\ Displaystyle A = Q \ Lambda Q ^ {- 1},}

o en cambio a la izquierda multiplicando ambos lados por Q ⁻¹ ,

{\ Displaystyle Q ^ {- 1} AQ = \ Lambda.}

Por tanto, A puede descomponerse en una matriz compuesta por sus autovectores, una matriz diagonal con sus autovalores a lo largo de la diagonal y la inversa de la matriz de autovectores. Esto se llama descomposición propia y es una transformación de similitud . Se dice que dicha matriz A es similar a la matriz diagonal Λ o diagonalizable . La matriz Q es la matriz de cambio de base de la transformación de similitud. Esencialmente, las matrices A y Λ representan la misma transformación lineal expresada en dos bases diferentes. Los vectores propios se utilizan como base al representar la transformación lineal como Λ.

A la inversa, suponga que una matriz A es diagonalizable. Deje que P sea una matriz cuadrada no singular tal que P ^-1AP es alguna matriz diagonal D . A la izquierda multiplicando ambos por P , AP = PD . Cada columna de P , por tanto, debe ser un vector propio de A cuyo valor propio es el elemento diagonal correspondiente de D . Dado que las columnas de P deben ser linealmente independientes para que P sea invertible, existen n vectores propios de A linealmente independientes . De ello se deduce que los autovectores de A forman una base si y solo si A es diagonalizable.

Se dice que una matriz que no es diagonalizable es defectuosa . Para matrices defectuosas, la noción de autovectores se generaliza a autovectores generalizados y la matriz diagonal de autovalores se generaliza a la forma normal de Jordan . Sobre un campo algebraicamente cerrado, cualquier matriz A tiene una forma normal de Jordan y, por lo tanto, admite una base de autovectores generalizados y una descomposición en autoespacios generalizados .

Caracterización variacional

En el caso de Hermitian , a los valores propios se les puede dar una caracterización variacional. El valor propio más grande de es el valor máximo de la forma cuadrática . Un valor de que se da cuenta de ese máximo, es un vector propio. ${\ Displaystyle H}$ ${\ Displaystyle \ mathbf {x} ^ {\ textsf {T}} H \ mathbf {x} / \ mathbf {x} ^ {\ textsf {T}} \ mathbf {x}}$ ${\ Displaystyle \ mathbf {x}}$

Ejemplos de matrices

Ejemplo de matriz bidimensional

La matriz de transformación A = conserva la dirección de los vectores de color púrpura paralelo a v _λ_{= 1} = [1 -1] ^T y vectores azules paralelos a v _λ_{= 3} = [1 1] ^T . Los vectores rojos no son paralelos a ninguno de los vectores propios, por lo que la transformación cambia sus direcciones. Las longitudes de los vectores púrpuras no cambian después de la transformación (debido a su valor propio de 1), mientras que los vectores azules tienen tres veces la longitud del original (debido a su valor propio de 3). Consulte también: Una versión extendida, que muestra los cuatro cuadrantes .

{\ Displaystyle \ left [{\ begin {smallmatrix} 2 & 1 \\ 1 & 2 \ end {smallmatrix}} \ right]}

Considere la matriz

{\ displaystyle A = {\ begin {bmatrix} 2 & 1 \\ 1 & 2 \ end {bmatrix}}.}

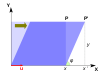
La figura de la derecha muestra el efecto de esta transformación en coordenadas de puntos en el plano. Los autovectores v de esta transformación satisfacen la ecuación ( 1 ), y los valores de λ para los cuales el determinante de la matriz ( A - λI ) es igual a cero son los autovalores.

Tomando el determinante para encontrar el polinomio característico de A ,

{\ displaystyle {\ begin {align} | A- \ lambda I | & = \ left | {\ begin {bmatrix} 2 & 1 \\ 1 & 2 \ end {bmatrix}} - \ lambda {\ begin {bmatrix} 1 & 0 \\ 0 & 1 \ end {bmatrix}} \ right | = {\ begin {vmatrix} 2- \ lambda & 1 \\ 1 & 2- \ lambda \ end {vmatrix}} \\ [6pt] & = 3-4 \ lambda + \ lambda ^ { 2}. \ End {alineado}}}

Ajuste de las raíces polinomio característico igual a cero, que tiene a λ = 1 y λ = 3 , que son los dos valores propios de A .

Para λ = 1 , la Ecuación ( 2 ) se convierte en,

{\ displaystyle (AI) \ mathbf {v} _ {\ lambda = 1} = {\ begin {bmatrix} 1 & 1 \\ 1 & 1 \ end {bmatrix}} {\ begin {bmatrix} v_ {1} \\ v_ {2 } \ end {bmatrix}} = {\ begin {bmatrix} 0 \\ 0 \ end {bmatrix}}}

{\ Displaystyle 1v_ {1} + 1v_ {2} = 0}

;

{\ Displaystyle 1v_ {1} + 1v_ {2} = 0}

Cualquier vector distinto de cero con v ₁ = - v ₂ resuelve esta ecuación. Por lo tanto,

{\ Displaystyle \ mathbf {v} _ {\ lambda = 1} = {\ begin {bmatrix} v_ {1} \\ - v_ {1} \ end {bmatrix}} = {\ begin {bmatrix} 1 \\ - 1 \ end {bmatrix}}}

es un vector propio de A correspondiente a λ = 1, al igual que cualquier múltiplo escalar de este vector.

Para λ = 3 , la ecuación ( 2 ) se convierte en

{\ Displaystyle {\ begin {alineado} (A-3I) \ mathbf {v} _ {\ lambda = 3} & = {\ begin {bmatrix} -1 & 1 \\ 1 & -1 \ end {bmatrix}} {\ begin {bmatrix} v_ {1} \\ v_ {2} \ end {bmatrix}} = {\ begin {bmatrix} 0 \\ 0 \ end {bmatrix}} \\ - 1v_ {1} + 1v_ {2} & = 0; \\ 1v_ {1} -1v_ {2} & = 0 \ end {alineado}}}

Cualquier vector distinto de cero con v ₁ = v ₂ resuelve esta ecuación. Por lo tanto,

{\ Displaystyle \ mathbf {v} _ {\ lambda = 3} = {\ begin {bmatrix} v_ {1} \\ v_ {1} \ end {bmatrix}} = {\ begin {bmatrix} 1 \\ 1 \ end {bmatrix}}}

es un vector propio de A correspondiente a λ = 3, al igual que cualquier múltiplo escalar de este vector.

Así, los vectores v _{λ = 1} y v _{λ = 3} son vectores propios de A asociados con los valores propios λ = 1 y λ = 3 , respectivamente.

Fórmula general para valores propios de una matriz bidimensional

Los valores propios de la matriz real son ${\ Displaystyle A = {\ begin {bmatrix} a & b \\ c & d \ end {bmatrix}}}$

{\ Displaystyle \ lambda = {\ frac {1} {2}} (a + d) \ pm {\ sqrt {\ left ({\ frac {1} {2}} (anuncio) \ right) ^ {2} + bc}} = {\ frac {1} {2}} \ left (\ operatorname {tr} (A) \ pm {\ sqrt {\ left (\ operatorname {tr} (A) ^ {2} \ right) -4 \ det (A)}} \ derecha).}

Tenga en cuenta que los valores propios son siempre reales si b y c tienen el mismo signo, ya que la cantidad bajo el radical debe ser positivo.

Ejemplo de matriz tridimensional

Considere la matriz

{\ displaystyle A = {\ begin {bmatrix} 2 & 0 & 0 \\ 0 & 3 & 4 \\ 0 & 4 & 9 \ end {bmatrix}}.}

El polinomio característico de A es

{\ displaystyle {\ begin {align} | A- \ lambda I | & = \ left | {\ begin {bmatrix} 2 & 0 & 0 \\ 0 & 3 & 4 \\ 0 & 4 & 9 \ end {bmatrix}} - \ lambda {\ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix}} \ right | = {\ begin {vmatrix} 2- \ lambda & 0 & 0 \\ 0 & 3- \ lambda & 4 \\ 0 & 4 & 9- \ lambda \ end {vmatrix}}, \\ [ 6pt] & = (2- \ lambda) {\ bigl [} (3- \ lambda) (9- \ lambda) -16 {\ bigr]} = - \ lambda ^ {3} +14 \ lambda ^ {2} -35 \ lambda +22. \ End {alineado}}}

Las raíces del polinomio característico son 2, 1, y 11, que son los únicos tres valores propios de A . Estos valores propios corresponden a los vectores propios , , y , o cualquier múltiplo no cero de los mismos. ${\ displaystyle {\ begin {bmatrix} 1 & 0 & 0 \ end {bmatrix}} ^ {\ textsf {T}}}$ ${\ displaystyle {\ begin {bmatrix} 0 & -2 & 1 \ end {bmatrix}} ^ {\ textsf {T}}}$ ${\ displaystyle {\ begin {bmatrix} 0 & 1 & 2 \ end {bmatrix}} ^ {\ textsf {T}}}$

Ejemplo de matriz tridimensional con valores propios complejos

Considere la matriz de permutación cíclica

{\ displaystyle A = {\ begin {bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \ end {bmatrix}}.}

Esta matriz desplaza las coordenadas del vector hacia arriba en una posición y mueve la primera coordenada hacia abajo. Su polinomio característico es 1 - λ ³ , cuyas raíces son

{\ Displaystyle {\ begin {alineado} \ lambda _ {1} & = 1 \\\ lambda _ {2} & = - {\ frac {1} {2}} + i {\ frac {\ sqrt {3} } {2}} \\\ lambda _ {3} & = \ lambda _ {2} ^ {*} = - {\ frac {1} {2}} - i {\ frac {\ sqrt {3}} { 2}} \ end {alineado}}}

donde es una unidad imaginaria con . ${\ Displaystyle i}$ ${\ Displaystyle i ^ {2} = - 1}$

Para el valor propio real λ ₁ = 1, cualquier vector con tres entradas iguales distintas de cero es un vector propio. Por ejemplo,

{\ displaystyle A {\ begin {bmatrix} 5 \\ 5 \\ 5 \ end {bmatrix}} = {\ begin {bmatrix} 5 \\ 5 \\ 5 \ end {bmatrix}} = 1 \ cdot {\ begin {bmatrix} 5 \\ 5 \\ 5 \ end {bmatrix}}.}

Para el par conjugado complejo de valores propios imaginarios,

{\ Displaystyle \ lambda _ {2} \ lambda _ {3} = 1, \ quad \ lambda _ {2} ^ {2} = \ lambda _ {3}, \ quad \ lambda _ {3} ^ {2} = \ lambda _ {2}.}

Luego

{\ displaystyle A {\ begin {bmatrix} 1 \\\ lambda _ {2} \\\ lambda _ {3} \ end {bmatrix}} = {\ begin {bmatrix} \ lambda _ {2} \\\ lambda _ {3} \\ 1 \ end {bmatrix}} = \ lambda _ {2} \ cdot {\ begin {bmatrix} 1 \\\ lambda _ {2} \\\ lambda _ {3} \ end {bmatrix} },}

y

{\ displaystyle A {\ begin {bmatrix} 1 \\\ lambda _ {3} \\\ lambda _ {2} \ end {bmatrix}} = {\ begin {bmatrix} \ lambda _ {3} \\\ lambda _ {2} \\ 1 \ end {bmatrix}} = \ lambda _ {3} \ cdot {\ begin {bmatrix} 1 \\\ lambda _ {3} \\\ lambda _ {2} \ end {bmatrix} }.}

Por lo tanto, los otros dos autovectores de A son complejos y son y con autovalores λ ₂ y λ ₃ , respectivamente. Los dos vectores propios complejos también aparecen en un par conjugado complejo, ${\ displaystyle \ mathbf {v} _ {\ lambda _ {2}} = {\ begin {bmatrix} 1 & \ lambda _ {2} & \ lambda _ {3} \ end {bmatrix}} ^ {\ textsf {T }}}$ ${\ displaystyle \ mathbf {v} _ {\ lambda _ {3}} = {\ begin {bmatrix} 1 & \ lambda _ {3} & \ lambda _ {2} \ end {bmatrix}} ^ {\ textsf {T }}}$

{\ Displaystyle \ mathbf {v} _ {\ lambda _ {2}} = \ mathbf {v} _ {\ lambda _ {3}} ^ {*}.}

Ejemplo de matriz diagonal

Las matrices con entradas solo a lo largo de la diagonal principal se denominan matrices diagonales . Los valores propios de una matriz diagonal son los propios elementos diagonales. Considere la matriz

{\ displaystyle A = {\ begin {bmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \ end {bmatrix}}.}

El polinomio característico de A es

{\ Displaystyle | A- \ lambda I | = (1- \ lambda) (2- \ lambda) (3- \ lambda),}

que tiene las raíces λ ₁ = 1 , λ ₂ = 2 y λ ₃ = 3 . Estas raíces son los elementos diagonales, así como los valores propios de A .

Cada elemento diagonal corresponde a un vector propio cuyo único componente distinto de cero está en la misma fila que ese elemento diagonal. En el ejemplo, los valores propios corresponden a los vectores propios,

{\ Displaystyle \ mathbf {v} _ {\ lambda _ {1}} = {\ begin {bmatrix} 1 \\ 0 \\ 0 \ end {bmatrix}}, \ quad \ mathbf {v} _ {\ lambda _ {2}} = {\ begin {bmatrix} 0 \\ 1 \\ 0 \ end {bmatrix}}, \ quad \ mathbf {v} _ {\ lambda _ {3}} = {\ begin {bmatrix} 0 \ \ 0 \\ 1 \ end {bmatrix}},}

respectivamente, así como múltiplos escalares de estos vectores.

Ejemplo de matriz triangular

Una matriz cuyos elementos por encima de la diagonal principal son todos cero se denomina matriz triangular inferior , mientras que una matriz cuyos elementos por debajo de la diagonal principal son todos cero se denomina matriz triangular superior . Al igual que con las matrices diagonales, los valores propios de las matrices triangulares son los elementos de la diagonal principal.

Considere la matriz triangular inferior,

{\ displaystyle A = {\ begin {bmatrix} 1 & 0 & 0 \\ 1 & 2 & 0 \\ 2 & 3 & 3 \ end {bmatrix}}.}

El polinomio característico de A es

{\ Displaystyle | A- \ lambda I | = (1- \ lambda) (2- \ lambda) (3- \ lambda),}

que tiene las raíces λ ₁ = 1 , λ ₂ = 2 y λ ₃ = 3 . Estas raíces son los elementos diagonales, así como los valores propios de A .

Estos autovalores corresponden a los autovectores,

{\ Displaystyle \ mathbf {v} _ {\ lambda _ {1}} = {\ begin {bmatrix} 1 \\ - 1 \\ {\ frac {1} {2}} \ end {bmatrix}}, \ quad \ mathbf {v} _ {\ lambda _ {2}} = {\ begin {bmatrix} 0 \\ 1 \\ - 3 \ end {bmatrix}}, \ quad \ mathbf {v} _ {\ lambda _ {3 }} = {\ begin {bmatrix} 0 \\ 0 \\ 1 \ end {bmatrix}},}

respectivamente, así como múltiplos escalares de estos vectores.

Ejemplo de matriz con valores propios repetidos

Como en el ejemplo anterior, la matriz triangular inferior

{\ displaystyle A = {\ begin {bmatrix} 2 & 0 & 0 & 0 \\ 1 & 2 & 0 & 0 \\ 0 & 1 & 3 & 0 \\ 0 & 0 & 1 & 3 \ end {bmatrix}},}

tiene un polinomio característico que es el producto de sus elementos diagonales,

{\ displaystyle | A- \ lambda I | = {\ begin {vmatrix} 2- \ lambda & 0 & 0 & 0 \\ 1 & 2- \ lambda & 0 & 0 \\ 0 & 1 & 3- \ lambda & 0 \\ 0 & 0 & 1 & 3- \ lambda \ end {vmatrix}} = ( 2- \ lambda) ^ {2} (3- \ lambda) ^ {2}.}

Las raíces de este polinomio, y por tanto los valores propios, son 2 y 3. La multiplicidad algebraica de cada valor propio es 2; en otras palabras, ambos son raíces dobles. La suma de las multiplicidades algebraicas de todos los valores propios distintos es μ _A = 4 = n , la orden del polinomio característico y la dimensión de A .

Por otro lado, la multiplicidad geométrica del valor propio 2 es solo 1, porque su espacio propio está dividido en un solo vector y, por lo tanto, es unidimensional. De manera similar, la multiplicidad geométrica del valor propio 3 es 1 porque su espacio propio está dividido en un solo vector . La multiplicidad geométrica total γ _A es 2, que es la más pequeña que podría ser para una matriz con dos valores propios distintos. Las multiplicidades geométricas se definen en una sección posterior. ${\ displaystyle {\ begin {bmatrix} 0 & 1 & -1 & 1 \ end {bmatrix}} ^ {\ textsf {T}}}$ ${\ displaystyle {\ begin {bmatrix} 0 & 0 & 0 & 1 \ end {bmatrix}} ^ {\ textsf {T}}}$

Identidad autovector-autovalor

Para una matriz hermitiana , la norma al cuadrado del j- ésimo componente de un vector propio normalizado se puede calcular utilizando solo los valores propios de la matriz y los valores propios de la matriz menor correspondiente ,

{\ Displaystyle | v_ {i, j} | ^ {2} = {\ frac {\ prod _ {k} {(\ lambda _ {i} - \ lambda _ {k} (M_ {j}))}} {\ prod _ {k \ neq i} {(\ lambda _ {i} - \ lambda _ {k})}}},}

donde es la submatriz formada al eliminar la j- ésima fila y columna de la matriz original. ${\ textstyle M_ {j}}$

Valores propios y funciones propias de operadores diferenciales

Las definiciones de autovalor y autovectores de una transformación lineal T siguen siendo válidas incluso si el espacio vectorial subyacente es un espacio de Hilbert o Banach de dimensión infinita . Una clase ampliamente utilizada de transformaciones lineales que actúan sobre espacios de dimensión infinita son los operadores diferenciales en espacios funcionales . Sea D un operador diferencial lineal en el espacio C ^∞ de funciones reales infinitamente diferenciables de un argumento real t . La ecuación de valor propio para D es la ecuación diferencial

{\ Displaystyle Df (t) = \ lambda f (t)}

Las funciones que satisfacen esta ecuación son vectores propios de D y se denominan comúnmente funciones propias .

Ejemplo de operador derivado

Considere el operador derivado con ecuación de valor propio ${\ Displaystyle {\ tfrac {d} {dt}}}$

{\ Displaystyle {\ frac {d} {dt}} f (t) = \ lambda f (t).}

Esta ecuación diferencial se puede resolver multiplicando ambos lados por dt / f ( t ) e integrando. Su solución, la función exponencial

{\ Displaystyle f (t) = f (0) e ^ {\ lambda t},}

es la función propia del operador derivado. En este caso, la función propia es en sí misma una función de su valor propio asociado. En particular, para λ = 0 la función propia f ( t ) es una constante.

El artículo principal sobre funciones propias ofrece otros ejemplos.

Definición general

El concepto de autovalores y autovectores se extiende naturalmente a transformaciones lineales arbitrarias en espacios vectoriales arbitrarios. Sea V cualquier espacio vectorial sobre algún campo K de escalares , y sea T una transformación lineal que mapee V en V ,

{\ Displaystyle T: V \ a V.}

Decimos que un vector distinto de cero v ∈ V es un vector propio de T si y solo si existe un escalar λ ∈ K tal que

{\ Displaystyle T (\ mathbf {v}) = \ lambda \ mathbf {v}.}

( 5 )

Esta ecuación se llama ecuación de valor propio para T , y el escalar λ es el valor propio de T correspondiente al vector propio v . T ( v ) es el resultado de aplicar la transformación T al vector v , mientras que λ v es el producto del escalar λ con v .

Espacios propios, multiplicidad geométrica y base propia

Dado un valor propio λ , considere el conjunto

{\ Displaystyle E = \ left \ {\ mathbf {v}: T (\ mathbf {v}) = \ lambda \ mathbf {v} \ right \},}

que es la unión del vector cero con el conjunto de todos los autovectores asociados con λ . E se denomina espacio propio o espacio característico de T asociado con λ .

Por definición de una transformación lineal,

{\ Displaystyle {\ begin {alineado} T (\ mathbf {x} + \ mathbf {y}) & = T (\ mathbf {x}) + T (\ mathbf {y}), \\ T (\ alpha \ mathbf {x}) & = \ alpha T (\ mathbf {x}), \ end {alineado}}}

para x , y ∈ V y alpha ∈ K . Por lo tanto, si u y v son vectores propios de T asociados con el valor propio λ , es decir , u , v ∈ E , entonces

{\ Displaystyle {\ begin {alineado} T (\ mathbf {u} + \ mathbf {v}) & = \ lambda (\ mathbf {u} + \ mathbf {v}), \\ T (\ alpha \ mathbf { v}) & = \ lambda (\ alpha \ mathbf {v}). \ end {alineado}}}

Entonces, tanto u + v como α v son cero o vectores propios de T asociados con λ , es decir, u + v , α v ∈ E , y E está cerrado bajo suma y multiplicación escalar. El espacio característico E asociado a λ , por tanto, es un subespacio lineal de V . Si ese subespacio tiene dimensión 1, a veces se denomina línea propia .

La multiplicidad geométrica γ _T ( λ ) de un valor propio λ es la dimensión del espacio propio asociado con λ , es decir, el número máximo de vectores propios linealmente independientes asociados con ese valor propio. Según la definición de autovalores y autovectores, γ _T ( λ ) ≥ 1 porque cada autovalor tiene al menos un autovector.

Los espacios propios de T siempre forman una suma directa . Como consecuencia, los autovectores de diferentes autovalores son siempre linealmente independientes. Por lo tanto, la suma de las dimensiones de los espacios propios no puede exceder la dimensión n del espacio vectorial en el que opera T , y no puede haber más de n valores propios distintos.

Cualquier subespacio generado por vectores propios de T es un subespacio invariante de T , y la restricción de T a tal subespacio es diagonalizable. Además, si todo el espacio vectorial V puede ser generado por los autovectores de T , o de manera equivalente si la suma directa de los autoespacios asociados con todos los autovalores de T es el espacio vectorial completo V , entonces una base de V llamada autobasis puede ser formado a partir de vectores propios linealmente independientes de T . Cuando T admite una base propia, T es diagonalizable.

Vector cero como vector propio

Si bien la definición de un vector propio utilizada en este artículo excluye el vector cero , es posible definir valores propios y vectores propios de modo que el vector cero sea un vector propio.

Considere nuevamente la ecuación de valor propio, Ecuación ( 5 ). Defina un valor propio como cualquier escalar λ ∈ K tal que exista un vector distinto de cero v ∈ V que satisfaga la Ecuación ( 5 ). Es importante que esta versión de la definición de un valor propio especifique que el vector sea distinto de cero; de lo contrario, según esta definición, el vector cero permitiría que cualquier escalar en K sea un valor propio. Defina un vector propio v asociado con el valor propio λ como cualquier vector que, dado λ , satisfaga la Ecuación ( 5 ). Dado el valor propio, el vector cero se encuentra entre los vectores que satisfacen la ecuación ( 5 ), por lo que el vector cero se incluye entre los vectores propios según esta definición alternativa.

Teoría espectral

Si λ es un valor propio de T , entonces el operador ( T - λI ) no es uno a uno y, por lo tanto, su inverso ( T - λI ) ⁻¹ no existe. Lo contrario es cierto para los espacios vectoriales de dimensión finita, pero no para los espacios vectoriales de dimensión infinita. En general, el operador ( T - λI ) puede no tener una inversa incluso si λ no es un valor propio.

Por esta razón, en el análisis funcional, los valores propios se pueden generalizar al espectro de un operador lineal T como el conjunto de todos los escalares λ para los cuales el operador ( T - λI ) no tiene inversa acotada . El espectro de un operador siempre contiene todos sus valores propios, pero no se limita a ellos.

Álgebras asociativas y teoría de la representación

Se puede generalizar el objeto algebraico que actúa sobre el espacio vectorial, reemplazando un solo operador que actúa sobre un espacio vectorial por una representación de álgebra : un álgebra asociativa que actúa sobre un módulo . El estudio de tales acciones es el campo de la teoría de la representación .

El concepto teórico de representación del peso es un análogo de los valores propios, mientras que los vectores de peso y los espacios de peso son los análogos de los vectores propios y los espacios propios, respectivamente.

Ecuaciones dinámicas

Las ecuaciones en diferencias más simples tienen la forma

{\ Displaystyle x_ {t} = a_ {1} x_ {t-1} + a_ {2} x_ {t-2} + \ cdots + a_ {k} x_ {tk}.}

La solución de esta ecuación para x en términos de t se encuentra usando su ecuación característica

{\ Displaystyle \ lambda ^ {k} -a_ {1} \ lambda ^ {k-1} -a_ {2} \ lambda ^ {k-2} - \ cdots -a_ {k-1} \ lambda -a_ { k} = 0,}

que se puede encontrar apilando en forma de matriz un conjunto de ecuaciones que consta de la ecuación en diferencias anterior y las ecuaciones k - 1 que dan un sistema k -dimensional de primer orden en el vector variable apilada en términos de su valor una vez rezagado, y tomando la ecuación característica de la matriz de este sistema. Esta ecuación da k raíces características para usar en la ecuación de solución. ${\ Displaystyle x_ {t-1} = x_ {t-1}, \ \ dots, \ x_ {t-k + 1} = x_ {t-k + 1},}$ ${\ Displaystyle {\ begin {bmatrix} x_ {t} & \ cdots & x_ {t-k + 1} \ end {bmatrix}}}$ ${\ Displaystyle \ lambda _ {1}, \, \ ldots, \, \ lambda _ {k},}$

{\ Displaystyle x_ {t} = c_ {1} \ lambda _ {1} ^ {t} + \ cdots + c_ {k} \ lambda _ {k} ^ {t}.}

Se utiliza un procedimiento similar para resolver una ecuación diferencial de la forma

{\ Displaystyle {\ frac {d ^ {k} x} {dt ^ {k}}} + a_ {k-1} {\ frac {d ^ {k-1} x} {dt ^ {k-1} }} + \ cdots + a_ {1} {\ frac {dx} {dt}} + a_ {0} x = 0.}

Cálculo

El cálculo de autovalores y autovectores es un tema en el que la teoría, como se presenta en los libros de texto de álgebra lineal elemental, a menudo está muy lejos de la práctica.

Método clásico

El método clásico consiste en encontrar primero los valores propios y luego calcular los vectores propios para cada valor propio. En varios sentidos, es poco adecuado para aritmética no exacta, como el punto flotante .

Autovalores

Los valores propios de una matriz se pueden determinar encontrando las raíces del polinomio característico. Esto es fácil para las matrices, pero la dificultad aumenta rápidamente con el tamaño de la matriz. ${\ Displaystyle A}$ ${\ Displaystyle 2 \ times 2}$

En teoría, los coeficientes del polinomio característico se pueden calcular con exactitud, ya que son sumas de productos de elementos de la matriz; y hay algoritmos que pueden encontrar todas las raíces de un polinomio de grado arbitrario con cualquier precisión requerida . Sin embargo, este enfoque no es viable en la práctica porque los coeficientes estarían contaminados por inevitables errores de redondeo , y las raíces de un polinomio pueden ser una función extremadamente sensible de los coeficientes (como lo ejemplifica el polinomio de Wilkinson ). Incluso para matrices cuyos elementos son números enteros, el cálculo no es trivial, porque las sumas son muy largas; el término constante es el determinante , que para an es una suma de diferentes productos. ${\ Displaystyle n \ times n}$ ${\ Displaystyle n!}$

Las fórmulas algebraicas explícitas para las raíces de un polinomio existen solo si el grado es 4 o menos. Según el teorema de Abel-Ruffini, no existe una fórmula algebraica general, explícita y exacta para las raíces de un polinomio con grado 5 o más. (La generalidad importa porque cualquier polinomio con grado es el polinomio característico de alguna matriz compañera de orden .) Por lo tanto, para matrices de orden 5 o más, los autovalores y autovectores no pueden obtenerse mediante una fórmula algebraica explícita y, por lo tanto, deben calcularse por aproximación métodos numéricos . Incluso la fórmula exacta para las raíces de un polinomio de grado 3 es numéricamente impráctica. ${\ Displaystyle n}$ ${\ Displaystyle n}$ ${\ Displaystyle n}$

Vectores propios

Una vez que se conoce el valor (exacto) de un valor propio, los vectores propios correspondientes se pueden encontrar al encontrar soluciones distintas de cero de la ecuación del valor propio, que se convierte en un sistema de ecuaciones lineales con coeficientes conocidos. Por ejemplo, una vez que se sabe que 6 es un valor propio de la matriz

{\ displaystyle A = {\ begin {bmatrix} 4 y 1 \\ 6 y 3 \ end {bmatrix}}}

podemos encontrar sus autovectores resolviendo la ecuación , es decir ${\ Displaystyle Av = 6v}$

{\ displaystyle {\ begin {bmatrix} 4 & 1 \\ 6 & 3 \ end {bmatrix}} {\ begin {bmatrix} x \\ y \ end {bmatrix}} = 6 \ cdot {\ begin {bmatrix} x \\ y \ end {bmatrix}}}

Esta ecuación matricial es equivalente a dos ecuaciones lineales

{\ Displaystyle \ left \ {{\ begin {alineado} 4x + y & = 6x \\ 6x + 3y & = 6y \ end {alineado}} \ right.}

es decir

{\ Displaystyle \ left \ {{\ begin {alineado} -2x + y & = 0 \\ 6x-3y & = 0 \ end {alineado}} \ right.}

Ambas ecuaciones se reducen a una única ecuación lineal . Por lo tanto, cualquier vector de la forma , para cualquier número real distinto de cero , es un vector propio de con valor propio . ${\ Displaystyle y = 2x}$ ${\ displaystyle {\ begin {bmatrix} a & 2a \ end {bmatrix}} ^ {\ textsf {T}}}$ ${\ Displaystyle a}$ ${\ Displaystyle A}$ ${\ Displaystyle \ lambda = 6}$

La matriz anterior tiene otro valor propio . Un cálculo similar muestra que los vectores propios correspondientes son las soluciones distintas de cero de , es decir, cualquier vector de la forma , para cualquier número real distinto de cero . ${\ Displaystyle A}$ ${\ Displaystyle \ lambda = 1}$ ${\ Displaystyle 3x + y = 0}$ ${\ displaystyle {\ begin {bmatrix} by -3b \ end {bmatrix}} ^ {\ textsf {T}}}$ ${\ Displaystyle b}$

Métodos iterativos simples

El enfoque inverso, de buscar primero los autovectores y luego determinar cada autovalor a partir de su autovector, resulta ser mucho más manejable para las computadoras. El algoritmo más fácil aquí consiste en elegir un vector inicial arbitrario y luego multiplicarlo repetidamente con la matriz (opcionalmente normalizar el vector para mantener sus elementos de tamaño razonable); esto hace que el vector converja hacia un vector propio. En cambio, una variación es multiplicar el vector por ; esto hace que converja a un vector propio del valor propio más cercano a . ${\ Displaystyle (A- \ mu I) ^ {- 1}}$ ${\ Displaystyle \ mu \ in \ mathbb {C}}$

Si es (una buena aproximación de) un vector propio de , entonces el valor propio correspondiente se puede calcular como ${\ Displaystyle \ mathbf {v}}$ ${\ Displaystyle A}$

{\ Displaystyle \ lambda = {\ frac {\ mathbf {v} ^ {*} A \ mathbf {v}} {\ mathbf {v} ^ {*} \ mathbf {v}}}}

donde denota la transposición conjugada de . ${\ Displaystyle \ mathbf {v} ^ {*}}$ ${\ Displaystyle \ mathbf {v}}$

Métodos modernos

Los métodos eficaces y precisos para calcular valores propios y vectores propios de matrices arbitrarias no se conocían hasta que se diseñó el algoritmo QR en 1961. La combinación de la transformación Householder con la descomposición LU da como resultado un algoritmo con mejor convergencia que el algoritmo QR. Para matrices dispersas hermitianas grandes , el algoritmo de Lanczos es un ejemplo de un método iterativo eficiente para calcular valores propios y vectores propios, entre varias otras posibilidades.

La mayoría de los métodos numéricos que calculan los valores propios de una matriz también determinan un conjunto de vectores propios correspondientes como subproducto del cálculo, aunque a veces los implementadores optan por descartar la información del vector propio tan pronto como ya no sea necesaria.

Aplicaciones

Autovalores de transformaciones geométricas

La siguiente tabla presenta algunos ejemplos de transformaciones en el plano junto con sus matrices 2 × 2, autovalores y autovectores.

	Escalada	Escala desigual	Rotación	Cizalla horizontal	Rotación hiperbólica
Ilustración
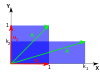
Matriz	${\ displaystyle {\ begin {bmatrix} k & 0 \\ 0 & k \ end {bmatrix}}}$	${\ displaystyle {\ begin {bmatrix} k_ {1} & 0 \\ 0 & k_ {2} \ end {bmatrix}}}$	${\ displaystyle {\ begin {bmatrix} c & -s \\ s & c \ end {bmatrix}}}$ ${\ Displaystyle c = \ cos \ theta}$ ${\ Displaystyle s = \ sin \ theta}$	${\ displaystyle {\ begin {bmatrix} 1 & k \\ 0 & 1 \ end {bmatrix}}}$	${\ displaystyle {\ begin {bmatrix} c & s \\ s & c \ end {bmatrix}}}$ ${\ Displaystyle c = \ cosh \ varphi}$ ${\ Displaystyle s = \ sinh \ varphi}$
Polinomio característico	${\ Displaystyle \ (\ lambda -k) ^ {2}}$	${\ Displaystyle (\ lambda -k_ {1}) (\ lambda -k_ {2})}$	${\ Displaystyle \ lambda ^ {2} -2c \ lambda +1}$	${\ Displaystyle \ (\ lambda -1) ^ {2}}$	${\ Displaystyle \ lambda ^ {2} -2c \ lambda +1}$
Autovalores, ${\ Displaystyle \ lambda _ {i}}$	${\ Displaystyle \ lambda _ {1} = \ lambda _ {2} = k}$	${\ Displaystyle \ lambda _ {1} = k_ {1}}$ ${\ Displaystyle \ lambda _ {2} = k_ {2}}$	${\ Displaystyle \ lambda _ {1} = e ^ {i \ theta} = c + si}$ ${\ Displaystyle \ lambda _ {2} = e ^ {- i \ theta} = c-si}$	${\ Displaystyle \ lambda _ {1} = \ lambda _ {2} = 1}$	${\ Displaystyle \ lambda _ {1} = e ^ {\ varphi} = c + s}$ ${\ Displaystyle \ lambda _ {2} = e ^ {- \ varphi} = cs}$
Mult algebraico . , ${\ Displaystyle \ mu _ {i} = \ mu (\ lambda _ {i})}$	${\ Displaystyle \ mu _ {1} = 2}$	${\ Displaystyle \ mu _ {1} = 1}$ ${\ Displaystyle \ mu _ {2} = 1}$	${\ Displaystyle \ mu _ {1} = 1}$ ${\ Displaystyle \ mu _ {2} = 1}$	${\ Displaystyle \ mu _ {1} = 2}$	${\ Displaystyle \ mu _ {1} = 1}$ ${\ Displaystyle \ mu _ {2} = 1}$
Mult geométrica . , ${\ Displaystyle \ gamma _ {i} = \ gamma (\ lambda _ {i})}$	${\ Displaystyle \ gamma _ {1} = 2}$	${\ Displaystyle \ gamma _ {1} = 1}$ ${\ Displaystyle \ gamma _ {2} = 1}$	${\ Displaystyle \ gamma _ {1} = 1}$ ${\ Displaystyle \ gamma _ {2} = 1}$	${\ Displaystyle \ gamma _ {1} = 1}$	${\ Displaystyle \ gamma _ {1} = 1}$ ${\ Displaystyle \ gamma _ {2} = 1}$
Vectores propios	Todos los vectores distintos de cero	${\ displaystyle {\ begin {alineado} \ mathbf {u} _ {1} & = {\ begin {bmatrix} 1 \\ 0 \ end {bmatrix}} \\\ mathbf {u} _ {2} & = { \ begin {bmatrix} 0 \\ 1 \ end {bmatrix}} \ end {alineado}}}$	${\ Displaystyle {\ begin {alineado} \ mathbf {u} _ {1} & = {\ begin {bmatrix} 1 \\ - i \ end {bmatrix}} \\\ mathbf {u} _ {2} & = {\ begin {bmatrix} 1 \\ + i \ end {bmatrix}} \ end {alineado}}}$	${\ Displaystyle \ mathbf {u} _ {1} = {\ begin {bmatrix} 1 \\ 0 \ end {bmatrix}}}$	${\ displaystyle {\ begin {alineado} \ mathbf {u} _ {1} & = {\ begin {bmatrix} 1 \\ 1 \ end {bmatrix}} \\\ mathbf {u} _ {2} & = { \ begin {bmatrix} 1 \\ - 1 \ end {bmatrix}}. \ end {alineado}}}$

La ecuación característica de una rotación es una ecuación cuadrática con discriminante , que es un número negativo siempre que $θ$ no es un múltiplo entero de 180 °. Por lo tanto, excepto en estos casos especiales, los dos valores propios son números complejos ; y todos los vectores propios tienen entradas no reales. De hecho, excepto en esos casos especiales, una rotación cambia la dirección de cada vector distinto de cero en el plano. ${\ Displaystyle D = -4 (\ sin \ theta) ^ {2}}$ ${\ Displaystyle \ cos \ theta \ pm i \ sin \ theta}$

Una transformación lineal que lleva un cuadrado a un rectángulo de la misma área (un mapeo de compresión ) tiene valores propios recíprocos.

Ecuación de Schrödinger

Las funciones de onda asociadas con los estados ligados de un electrón en un átomo de hidrógeno pueden verse como los vectores propios del Hamiltoniano del átomo de hidrógeno , así como del operador del momento angular . Están asociados con valores propios interpretados como sus energías (aumentando hacia abajo :) y momento angular (aumentando a través de: s, p, d,…). La ilustración muestra el cuadrado del valor absoluto de las funciones de onda. Las áreas más brillantes corresponden a una densidad de probabilidad más alta para una medición de posición . El centro de cada figura es el núcleo atómico , un protón .

{\ Displaystyle n = 1, \, 2, \, 3, \, \ ldots}

Un ejemplo de una ecuación de valor propio donde la transformación se representa en términos de un operador diferencial es la ecuación de Schrödinger independiente del tiempo en mecánica cuántica : ${\ Displaystyle T}$

{\ Displaystyle H \ psi _ {E} = E \ psi _ {E} \,}

donde , el hamiltoniano , es un operador diferencial de segundo orden y , la función de onda , es una de sus funciones propias correspondiente al valor propio , interpretado como su energía . ${\ Displaystyle H}$ ${\ Displaystyle \ psi _ {E}}$ ${\ Displaystyle E}$

Sin embargo, en el caso en el que a uno solo le interesan las soluciones de estado ligado de la ecuación de Schrödinger, se buscan dentro del espacio de funciones cuadradas integrables . Dado que este espacio es un espacio de Hilbert con un producto escalar bien definido , se puede introducir un conjunto de bases en el que y se puede representar como una matriz unidimensional (es decir, un vector) y una matriz, respectivamente. Esto permite representar la ecuación de Schrödinger en forma de matriz. ${\ Displaystyle \ psi _ {E}}$ ${\ Displaystyle \ psi _ {E}}$ ${\ Displaystyle H}$

La notación bra-ket se usa a menudo en este contexto. Un vector, que representa un estado del sistema, en el espacio de Hilbert de funciones cuadradas integrables está representado por . En esta notación, la ecuación de Schrödinger es: ${\ Displaystyle | \ Psi _ {E} \ rangle}$

{\ Displaystyle H | \ Psi _ {E} \ rangle = E | \ Psi _ {E} \ rangle}

donde es un estado propio de y representa el valor propio. es un operador autoadjunto observable , el análogo de dimensión infinita de las matrices hermitianas. Al igual que en el caso de la matriz, en la ecuación anterior se entiende que es el vector obtenido por aplicación de la transformación a . ${\ Displaystyle | \ Psi _ {E} \ rangle}$ ${\ Displaystyle H}$ ${\ Displaystyle E}$ ${\ Displaystyle H}$ ${\ Displaystyle H | \ Psi _ {E} \ rangle}$ ${\ Displaystyle H}$ ${\ Displaystyle | \ Psi _ {E} \ rangle}$

Transporte de olas

La luz , las ondas acústicas y las microondas se dispersan al azar numerosas veces al atravesar un sistema desordenado estático . Aunque la dispersión múltiple aleatoriza repetidamente las ondas, en última instancia, el transporte coherente de ondas a través del sistema es un proceso determinista que puede describirse mediante una matriz de transmisión de campo . Los vectores propios del operador de transmisión forman un conjunto de frentes de onda de entrada específicos del desorden que permiten que las ondas se acoplen a los canales propios del sistema desordenado: las vías independientes las ondas pueden viajar a través del sistema. Los valores propios`` de corresponden a la transmitancia de intensidad asociada con cada canal propio. Una de las propiedades notables del operador de transmisión de sistemas difusivos es su distribución bimodal de valores propios con y . Además, una de las propiedades sorprendentes de los canales propios abiertos, más allá de la transmitancia perfecta, es el perfil espacial estadísticamente robusto de los canales propios. ${\ Displaystyle \ mathbf {t}}$ ${\ Displaystyle \ mathbf {t} ^ {\ dagger} \ mathbf {t}}$ ${\ Displaystyle \ tau}$ ${\ Displaystyle \ mathbf {t} ^ {\ dagger} \ mathbf {t}}$ ${\ Displaystyle \ tau _ {\ max} = 1}$ ${\ Displaystyle \ tau _ {\ min} = 0}$

Orbitales moleculares

En la mecánica cuántica , y en particular en la física atómica y molecular , dentro de la teoría de Hartree-Fock , los orbitales atómicos y moleculares pueden definirse mediante los vectores propios del operador de Fock . Los valores propios correspondientes se interpretan como potenciales de ionización a través del teorema de Koopmans . En este caso, el término autovector se usa en un significado algo más general, ya que el operador de Fock depende explícitamente de los orbitales y sus autovalores. Así, si se quiere subrayar este aspecto, se habla de problemas de valores propios no lineales. Estas ecuaciones suelen resolverse mediante un procedimiento de iteración , denominado en este caso método de campo autoconsistente . En química cuántica , a menudo se representa la ecuación de Hartree-Fock en un conjunto de bases no ortogonales . Esta representación particular es un problema de valor propio generalizado llamado ecuaciones de Roothaan .

Geología y glaciología

En geología , especialmente en el estudio de la labranza glacial , los autovectores y autovalores se utilizan como un método mediante el cual una masa de información de la orientación y el buzamiento de los constituyentes de un tejido de clastos se puede resumir en un espacio tridimensional con seis números. En el campo, un geólogo puede recopilar dichos datos para cientos o miles de clastos en una muestra de suelo, que solo se pueden comparar gráficamente, como en un diagrama Tri-Plot (Sneed and Folk), o como Stereonet en una Wulff Net.

La salida para el tensor de orientación está en los tres ejes ortogonales (perpendiculares) del espacio. Los tres autovectores están ordenados por sus autovalores ; luego es la orientación / inmersión primaria del clast, es la secundaria y es la terciaria, en términos de resistencia. La orientación del clastos se define como la dirección del vector propio, en una rosa de los vientos de 360 ° . La caída se mide como el valor propio, el módulo del tensor: se valora de 0 ° (sin caída) a 90 ° (vertical). Los valores relativos de , y están dictados por la naturaleza del tejido del sedimento. Si , se dice que la tela es isotrópica. Si , se dice que la tela es plana. Si , se dice que la tela es lineal. ${\ Displaystyle \ mathbf {v} _ {1}, \ mathbf {v} _ {2}, \ mathbf {v} _ {3}}$ ${\ Displaystyle E_ {1} \ geq E_ {2} \ geq E_ {3}}$ ${\ Displaystyle \ mathbf {v} _ {1}}$ ${\ Displaystyle \ mathbf {v} _ {2}}$ ${\ Displaystyle \ mathbf {v} _ {3}}$ ${\ Displaystyle E_ {1}}$ ${\ Displaystyle E_ {2}}$ ${\ Displaystyle E_ {3}}$ ${\ Displaystyle E_ {1} = E_ {2} = E_ {3}}$ ${\ Displaystyle E_ {1} = E_ {2}> E_ {3}}$ ${\ Displaystyle E_ {1}> E_ {2}> E_ {3}}$

Análisis de componentes principales

PCA de la distribución gaussiana multivariante centrada en con una desviación estándar de 3 aproximadamente en la dirección y de 1 en la dirección ortogonal. Los vectores mostrados son vectores propios unitarios de la matriz de covarianza (simétrica, positiva-semidefinida) escalada por la raíz cuadrada del valor propio correspondiente. Al igual que en el caso unidimensional, la raíz cuadrada se toma porque la desviación estándar se visualiza más fácilmente que la varianza .

{\ Displaystyle (1,3)}

{\ displaystyle (0.878,0.478)}

La descomposición propia de una matriz semidefinita positiva simétrica (PSD) produce una base ortogonal de vectores propios, cada uno de los cuales tiene un valor propio no negativo. La descomposición ortogonal de una matriz PSD se utiliza en análisis multivariante , donde las matrices de covarianza de muestra son PSD. Esta descomposición ortogonal se denomina análisis de componentes principales (PCA) en estadística. PCA estudia relaciones lineales entre variables. El PCA se realiza en la matriz de covarianza o la matriz de correlación (en la que cada variable se escala para que su varianza muestral sea igual a uno). Para la matriz de covarianza o correlación, los autovectores corresponden a los componentes principales y los autovalores a la varianza explicada por los componentes principales. El análisis de componentes principales de la matriz de correlación proporciona una base ortogonal para el espacio de los datos observados: en esta base, los valores propios más grandes corresponden a los componentes principales que están asociados con la mayor parte de la covariabilidad entre varios datos observados.

El análisis de componentes principales se utiliza como un medio de reducción de dimensionalidad en el estudio de grandes conjuntos de datos , como los que se encuentran en bioinformática . En la metodología Q , los valores propios de la matriz de correlación determinan el juicio de importancia práctica del metodólogo Q (que difiere de la significancia estadística de la prueba de hipótesis ; cf. criterios para determinar el número de factores ). De manera más general, el análisis de componentes principales se puede utilizar como método de análisis factorial en el modelado de ecuaciones estructurales .

Análisis de vibraciones

Forma de modo de un diapasón a frecuencia propia 440,09 Hz

Los problemas de valores propios ocurren naturalmente en el análisis de vibraciones de estructuras mecánicas con muchos grados de libertad . Los valores propios son las frecuencias naturales (o frecuencias propias ) de vibración, y los vectores propios son las formas de estos modos vibratorios. En particular, la vibración no amortiguada se rige por

{\ Displaystyle m {\ ddot {x}} + kx = 0}

o

{\ Displaystyle m {\ ddot {x}} = - kx}

es decir, la aceleración es proporcional a la posición (es decir, esperamos que sea sinusoidal en el tiempo). ${\ Displaystyle x}$

En dimensiones, se convierte en una matriz de masa y una matriz de rigidez . Las soluciones admisibles son entonces una combinación lineal de soluciones al problema de valores propios generalizados ${\ Displaystyle n}$ ${\ Displaystyle m}$ ${\ Displaystyle k}$

{\ Displaystyle kx = \ omega ^ {2} mx}

donde es el valor propio y es la frecuencia angular (imaginaria) . Los principales modos de vibración son diferentes de los principales modos de cumplimiento, que son los vectores propios de solo. Además, la vibración amortiguada , gobernada por ${\ Displaystyle \ omega ^ {2}}$ ${\ Displaystyle \ omega}$ ${\ Displaystyle k}$

{\ Displaystyle m {\ ddot {x}} + c {\ dot {x}} + kx = 0}

conduce a un problema de valores propios cuadráticos ,

{\ Displaystyle \ left (\ omega ^ {2} m + \ omega c + k \ right) x = 0.}

Esto puede reducirse a un problema de valor propio generalizado mediante la manipulación algebraica a costa de resolver un sistema más grande.

Las propiedades de ortogonalidad de los autovectores permiten el desacoplamiento de las ecuaciones diferenciales para que el sistema se pueda representar como suma lineal de los autovectores. El problema del valor propio de las estructuras complejas a menudo se resuelve mediante el análisis de elementos finitos , pero generaliza claramente la solución a los problemas de vibración con valores escalares.

Caras propias

Caras propias como ejemplos de vectores propios

En el procesamiento de imágenes, las imágenes procesadas de caras pueden verse como vectores cuyos componentes son los brillos de cada píxel . La dimensión de este espacio vectorial es el número de píxeles. Los vectores propios de la matriz de covarianza asociados con un gran conjunto de imágenes normalizadas de caras se denominan caras propias ; este es un ejemplo de análisis de componentes principales . Son muy útiles para expresar cualquier imagen de rostro como una combinación lineal de algunos de ellos. En la rama de reconocimiento facial de la biometría , las caras propias proporcionan un medio para aplicar compresión de datos a las caras con fines de identificación . También se han realizado investigaciones relacionadas con los sistemas de visión propios que determinan los gestos de las manos.

De manera similar a este concepto, las voces propias representan la dirección general de variabilidad en las pronunciaciones humanas de un enunciado particular, como una palabra en un idioma. Sobre la base de una combinación lineal de tales voces propias, se puede construir una nueva pronunciación de la palabra. Estos conceptos se han encontrado útiles en sistemas de reconocimiento automático de voz para la adaptación del hablante.

Tensor de momento de inercia

En mecánica , los vectores propios del tensor del momento de inercia definen los ejes principales de un cuerpo rígido . El tensor de momento de inercia es una cantidad clave necesaria para determinar la rotación de un cuerpo rígido alrededor de su centro de masa .

Medidor de estrés

En mecánica de sólidos , el tensor de tensión es simétrico y, por lo tanto, puede descomponerse en un tensor diagonal con los valores propios en la diagonal y los vectores propios como base. Debido a que es diagonal, en esta orientación, el tensor de esfuerzos no tiene componentes de cortante ; los componentes que tiene son los componentes principales.

Gráficos

En la teoría de grafos espectrales , un valor propio de un gráfico se define como un valor propio de la matriz de adyacencia del gráfico , o (cada vez más) de la matriz laplaciana del gráfico debido a su operador de Laplace discreto , que es (a veces llamado laplaciano combinatorio ) o (a veces llamado laplaciano normalizado ), donde es una matriz diagonal con igual al grado de vértice , y en , la entrada diagonal es . El vector propio principal de un gráfico se define como el vector propio correspondiente al valor propio más grande o el más pequeño del laplaciano. El primer vector propio principal del gráfico también se denomina simplemente vector propio principal. ${\ Displaystyle A}$ ${\ Displaystyle DA}$ ${\ Displaystyle ID ^ {- 1/2} AD ^ {- 1/2}}$ ${\ Displaystyle D}$ ${\ Displaystyle D_ {ii}}$ ${\ Displaystyle v_ {i}}$ ${\ Displaystyle D ^ {- 1/2}}$ ${\ Displaystyle i}$ ${\ textstyle 1 / {\ sqrt {\ deg (v_ {i})}}}$ ${\ Displaystyle k}$ ${\ Displaystyle k}$ ${\ Displaystyle k}$

El vector propio principal se utiliza para medir la centralidad de sus vértices. Un ejemplo es el algoritmo PageRank de Google . El vector propio principal de una matriz de adyacencia modificada del gráfico de la World Wide Web da la clasificación de la página como sus componentes. Este vector corresponde a la distribución estacionaria de la cadena de Markov representada por la matriz de adyacencia normalizada por filas; sin embargo, la matriz de adyacencia debe modificarse primero para garantizar que exista una distribución estacionaria. El segundo vector propio más pequeño se puede utilizar para dividir el gráfico en grupos, mediante agrupamiento espectral . También hay otros métodos disponibles para la agrupación.

Número de reproducción básico

El número de reproducción básico ( ) es un número fundamental en el estudio de cómo se propagan las enfermedades infecciosas. Si una persona infecciosa se incluye en una población de personas completamente susceptibles, entonces es el número promedio de personas que una persona infecciosa típica infectará. El tiempo de generación de una infección es el tiempo, desde que una persona se infecta hasta que la siguiente se infecta. En una población heterogénea, la matriz de la próxima generación define cuántas personas de la población se infectarán una vez transcurrido el tiempo . es entonces el valor propio más grande de la matriz de la próxima generación. ${\ Displaystyle R_ {0}}$ ${\ Displaystyle R_ {0}}$ ${\ Displaystyle t_ {G}}$ ${\ Displaystyle t_ {G}}$ ${\ Displaystyle R_ {0}}$

Ver también

Notas

Citas

Fuentes

Akivis, Max A .; Goldberg, Vladislav V. (1969), cálculo de tensores , ruso, Science Publishers, Moscú
Aldrich, John (2006), "Valor propio, función propia, vector propio y términos relacionados" , en Miller, Jeff (ed.), Primeros usos conocidos de algunas de las palabras de las matemáticas
Alexandrov, Pavel S. (1968), Lecture notes in Analytical Geometry , Ruso, Science Publishers, Moscú
Anton, Howard (1987), Álgebra lineal elemental (5.a ed.), Nueva York: Wiley , ISBN 0-471-84819-0
Axler, Sheldon (18 de julio de 2017), Linear Algebra Done Right (3.a ed.), Springer, p. 77, ISBN 978-3-319-30765-7
Beauregard, Raymond A .; Fraleigh, John B. (1973), Un primer curso de álgebra lineal: con introducción opcional a grupos, anillos y campos , Boston: Houghton Mifflin Co. , ISBN 0-395-14017-X
Beezer, Robert A. (2006), Un primer curso de álgebra lineal , Libro en línea gratuito con licencia GNU, Universidad de Puget Sound
Benn, D .; Evans, D. (2004), Una guía práctica para el estudio de los sedimentos glaciales , Londres: Arnold, págs. 103-107
Betteridge, Harold T. (1965), The New Cassell's German Dictionary , Nueva York: Funk & Wagnall , LCCN 58-7924
Bowen, Ray M .; Wang, Chao-Cheng (1980), Álgebra lineal y multilineal , Plenum Press, Nueva York, ISBN 0-306-37508-7
Burden, Richard L .; Faires, J. Douglas (1993), Análisis numérico (5.a ed.), Boston: Prindle, Weber y Schmidt , ISBN 0-534-93219-3
Carter, Tamara A .; Tapia, Richard A .; Papaconstantinou, Anne, Linear Algebra: An Introduction to Linear Algebra for Pre-Calculus Students , Rice University, edición en línea , consultado el 19 de febrero de 2008
Cohen-Tannoudji, Claude (1977), "Capítulo II. Las herramientas matemáticas de la mecánica cuántica", Mecánica cuántica , John Wiley & Sons, ISBN 0-471-16432-1
Curtis, Charles W. (1999), Álgebra lineal: un enfoque introductorio (4a ed.), Springer, ISBN 0-387-90992-3
Demmel, James W. (1997), Álgebra lineal numérica aplicada , SIAM, ISBN 0-89871-389-7
Denton, Peter B .; Parke, Stephen J .; Tao, Terence; Zhang, Xining (2021). "Autovectores de autovalores: un estudio de una identidad básica en álgebra lineal". Boletín de la Sociedad Matemática Estadounidense : 1. arXiv : 1908.03795 . doi : 10.1090 / toro / 1722 . S2CID 213918682 .
Diekmann O, Heesterbeek JA, Metz JA (1990), "Sobre la definición y el cálculo de la tasa de reproducción básica R0 en modelos de enfermedades infecciosas en poblaciones heterogéneas", Journal of Mathematical Biology , 28 (4): 365–382, doi : 10.1007 / BF00178324 , hdl : 1874/8051 , PMID 2117040 , S2CID 22275430
Fraleigh, John B. (1976), Un primer curso de álgebra abstracta (2a ed.), Lectura: Addison-Wesley , ISBN 0-201-01984-1
Fraleigh, John B .; Beauregard, Raymond A. (1995), Álgebra lineal (3.a ed.), Addison-Wesley Publishing Company, ISBN 0-201-83999-7
Francis, JGF (1961), "The QR Transformation, I (part 1)", The Computer Journal , 4 (3): 265-271, doi : 10.1093 / comjnl / 4.3.265y Francis, JGF (1962), "The QR Transformation, II (part 2)", The Computer Journal , 4 (4): 332–345, doi : 10.1093 / comjnl / 4.4.332
Francis, JGF (1962), "The QR Transformation, II (part 2)", The Computer Journal , 4 (4): 332–345, doi : 10.1093 / comjnl / 4.4.332
Friedberg, Stephen H .; Insel, Arnold J .; Spence, Lawrence E. (1989), Álgebra lineal (2a ed.), Englewood Cliffs, Nueva Jersey: Prentice Hall, ISBN 0-13-537102-3
Gelfand, IM (1971), Lecture notes in linear álgebra , Ruso, Science Publishers, Moscú
Gohberg, Israel; Lancaster, Peter; Rodman, Leiba (2005), Álgebra lineal indefinida y aplicaciones , Basilea, Boston, Berlín: Birkhäuser Verlag, ISBN 3-7643-7349-0
Golub, Gene F .; van der Vorst, Henk A. (2000), "Cálculo de valores propios en el siglo XX" (PDF) , Journal of Computational and Applied Mathematics , 123 (1–2): 35–65, Bibcode : 2000JCoAM.123 ... 35G , doi : 10.1016 / S0377-0427 (00) 00413-1 , hdl : 1874/2663
Golub, Gene H .; Van Loan, Charles F. (1996), cálculos matriciales (3.a ed.), Baltimore, MD: Johns Hopkins University Press, ISBN 978-0-8018-5414-9
Graham, D .; Midgley, N. (2000), "Representación gráfica de la forma de partículas usando diagramas triangulares: un método de hoja de cálculo de Excel", Earth Surface Processes and Landforms , 25 (13): 1473–1477, Bibcode : 2000ESPL ... 25.1473G , doi : 10.1002 / 1096-9837 (200012) 25:13 <1473 :: AID-ESP158> 3.0.CO; 2-C , S2CID 128825838
Greub, Werner H. (1975), Álgebra lineal (4a ed.), Nueva York: Springer-Verlag, ISBN 0-387-90110-8
Halmos, Paul R. (1987), Espacios vectoriales de dimensión finita (8a ed.), Nueva York: Springer-Verlag, ISBN 0-387-90093-4
Hawkins, T. (1975), "Cauchy y la teoría espectral de matrices", Historia Mathematica , 2 : 1–29, doi : 10.1016 / 0315-0860 (75) 90032-4
Heesterbeek, JAP; Diekmann, Odo (2000), Epidemiología matemática de enfermedades infecciosas , serie de Wiley en biología matemática y computacional, West Sussex, Inglaterra: John Wiley & Sons
Hefferon, Jim (2001), Álgebra lineal , Colchester, VT: Libro en línea, St Michael's College
Herstein, IN (1964), Temas de álgebra , Waltham: Blaisdell Publishing Company , ISBN 978-1114541016
Horn, Roger A .; Johnson, Charles F. (1985), análisis de matrices , Cambridge University Press, ISBN 0-521-30586-1
Kline, Morris (1972), Pensamiento matemático desde la antigüedad hasta la época moderna , Oxford University Press, ISBN 0-19-501496-0
Knox-Robinson, C .; Gardoll, Stephen J. (1998), "GIS-stereoplot: an stereonet plotting module interactivo para el sistema de información geográfica ArcView 3.0", Computers & Geosciences , 24 (3): 243, Bibcode : 1998CG ..... 24..243K , doi : 10.1016 / S0098-3004 (97) 00122-2
Korn, Granino A .; Korn, Theresa M. (2000), "Manual matemático para científicos e ingenieros: Definiciones, teoremas y fórmulas de referencia y revisión", Nueva York: McGraw-Hill (segunda edición revisada), Bibcode : 1968mhse.book ... ..K , ISBN 0-486-41147-8
Kublanovskaya, Vera N. (1961), "Sobre algunos algoritmos para la solución del problema de valor propio completo", URSS Computational Mathematics and Mathematical Physics , 3 : 637–657. También publicado en: "О некоторых алгорифмах для решения полной проблемы собственных значений " [On ciertos algoritmos para la solución del problema de valor propio completa], Журнал вычислительной математики и математической физики (Journal of Computational Matemáticas y Física Matemática) (en ruso), 1 (4): 555–570, 1961
Kuttler, Kenneth (2007), Introducción al álgebra lineal (PDF) , Universidad Brigham Young
Lancaster, P. (1973), teoría de matrices , ruso, Moscú: Science Publishers
Larson, Ron; Edwards, Bruce H. (2003), Álgebra lineal elemental (5.a ed.), Houghton Mifflin Company, ISBN 0-618-33567-6
Lipschutz, Seymour (1991), esquema de la teoría y problemas de álgebra lineal de Schaum, serie de esquemas de Schaum (2a ed.), Nueva York: McGraw-Hill Companies, ISBN 0-07-038007-4
Lipschutz, Seymour; Lipson, Marc (12 de agosto de 2002). Esquema fácil de álgebra lineal de Schaum . Profesional de McGraw Hill. pag. 111. ISBN 978-007139880-0.
Meyer, Carl D. (2000), Análisis de matrices y álgebra lineal aplicada , Filadelfia: Sociedad de Matemáticas Industriales y Aplicadas (SIAM), ISBN 978-0-89871-454-8
Nering, Evar D. (1970), Álgebra lineal y teoría de matrices (2a ed.), Nueva York: Wiley , LCCN 76091646
Prensa, William H .; Teukolsky, Saul A .; Vetterling, William T .; Flannery, Brian P. (2007), Recetas numéricas: El arte de la informática científica (3.a ed.), ISBN 978-0521880688
Roman, Steven (2008), Álgebra lineal avanzada (3.a ed.), Nueva York: Springer Science + Business Media, ISBN 978-0-387-72828-5
Sharipov, Ruslan A. (1996), Curso de álgebra lineal y geometría multidimensional: el libro de texto , arXiv : math / 0405323 , Bibcode : 2004math ...... 5323S , ISBN 5-7477-0099-5
Shilov, Georgi E. (1977), Álgebra lineal , Traducido y editado por Richard A. Silverman, Nueva York: Dover Publications, ISBN 0-486-63518-X
Shores, Thomas S. (2007), álgebra lineal aplicada y análisis matricial , Springer Science + Business Media, ISBN 978-0-387-33194-2
Sneed, ED; Folk, RL (1958), "Guijarros en la parte baja del río Colorado, Texas, un estudio de la morfogénesis de partículas", Journal of Geology , 66 (2): 114-150, Bibcode : 1958JG ..... 66..114S , doi : 10.1086 / 626490 , S2CID 129658242
Strang, Gilbert (1993), Introducción al álgebra lineal , Wellesley, MA: Wellesley-Cambridge Press, ISBN 0-9614088-5-5
Strang, Gilbert (2006), Álgebra lineal y sus aplicaciones , Belmont, CA: Thomson, Brooks / Cole, ISBN 0-03-010567-6
Trefethen, Lloyd N .; Bau, David (1997), Álgebra lineal numérica , SIAM
Van Mieghem, Piet (18 de enero de 2014). "Graficar vectores propios, pesos fundamentales y métricas de centralidad para nodos en redes". arXiv : 1401.4580 [ math.SP ].
Weisstein, Eric W. "Eigenvector" . mathworld.wolfram.com . Consultado el 4 de agosto de 2019 .
Wolchover, Natalie (13 de noviembre de 2019). "Los neutrinos conducen a un descubrimiento inesperado en matemáticas básicas" . Revista Quanta . Consultado el 27 de noviembre de 2019 .
Xirouhakis, A .; Votsis, G .; Delopoulus, A. (2004), Estimación del movimiento 3D y la estructura de rostros humanos (PDF) , Universidad Técnica Nacional de Atenas
(en ruso) Pigolkina, TS; Shulman, VS (1977). "Valor propio". En Vinogradov, IM (ed.). Enciclopedia matemática . 5 . Moscú: Enciclopedia soviética.

Otras lecturas

"Una guía para principiantes de vectores propios" . Deeplearning4j . 2015. Archivado desde el original el 21 de julio de 2018 . Consultado el 18 de agosto de 2015 .
Hill, Roger (2009). "λ - Autovalores" . Sesenta símbolos . Brady Haran para la Universidad de Nottingham .

enlaces externos

¿Qué son los valores propios? - introducción no técnica de "Pregunte a los expertos" de PhysLink.com
Ejemplos numéricos de valores propios y vectores propios: programa tutorial y interactivo de Revoledu.
Introducción a los vectores propios y los valores propios : conferencia de Khan Academy
Autovectores y autovalores | Esencia del álgebra lineal, capítulo 10 - Una explicación visual con 3Blue1Brown
Calculadora de vectores propios de matrices de Symbolab (Haga clic en el botón inferior derecho de la cuadrícula de 2x12 para seleccionar un tamaño de matriz. Seleccione un tamaño (para una matriz cuadrada), luego complete las entradas numéricamente y haga clic en el botón Ir. Puede aceptar números complejos así como.) ${\ Displaystyle n \ times n}$

Teoría

"Valor propio" , Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
"Vector propio" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
"Valor propio (de una matriz)" . PlanetMath .
Vector propio - Wolfram MathWorld
Subprograma de trabajo Eigen Vector Examination
El mismo examen de vector propio que el anterior en una demostración de Flash con sonido
Cálculo de valores propios
Solución numérica de problemas de valores propios Editado por Zhaojun Bai, James Demmel , Jack Dongarra, Axel Ruhe y Henk van der Vorst
Autovalores y autovectores en los foros de Ask Dr. Math: [1] , [2]

Languages

In other projects

Valores propios y vectores propios - Eigenvalues and eigenvectors

Definicion formal

Visión general

Historia

Autovalores y autovectores de matrices

Autovalores y el polinomio característico

Multiplicidad algebraica

Espacios propios, multiplicidad geométrica y base propia para matrices

Propiedades adicionales de los valores propios

Vectores propios izquierdo y derecho

Diagonalización y autodescomposición

Caracterización variacional

Ejemplos de matrices

Ejemplo de matriz bidimensional

Fórmula general para valores propios de una matriz bidimensional

Ejemplo de matriz tridimensional

Ejemplo de matriz tridimensional con valores propios complejos

Ejemplo de matriz diagonal

Ejemplo de matriz triangular

Ejemplo de matriz con valores propios repetidos

Identidad autovector-autovalor

Valores propios y funciones propias de operadores diferenciales

Ejemplo de operador derivado

Definición general

Espacios propios, multiplicidad geométrica y base propia

Vector cero como vector propio

Teoría espectral

Álgebras asociativas y teoría de la representación

Ecuaciones dinámicas

Cálculo

Método clásico

Autovalores

Vectores propios

Métodos iterativos simples

Métodos modernos

Aplicaciones

Autovalores de transformaciones geométricas

Ecuación de Schrödinger

Transporte de olas

Orbitales moleculares

Geología y glaciología

Análisis de componentes principales

Análisis de vibraciones

Caras propias

Tensor de momento de inercia

Medidor de estrés

Gráficos

Número de reproducción básico

Ver también

Notas

Citas

Fuentes

Otras lecturas

enlaces externos

Teoría